Understanding the Venturi Effect: Solving Equations for Ideal Liquid Flow

[Olly Vogel]

Hello everyone :)

I was given a problem reguarding Venturi effect. By a coincidence, I found a youtube video which solves the same question, but I didn't undersand one of its equations.
The problem:

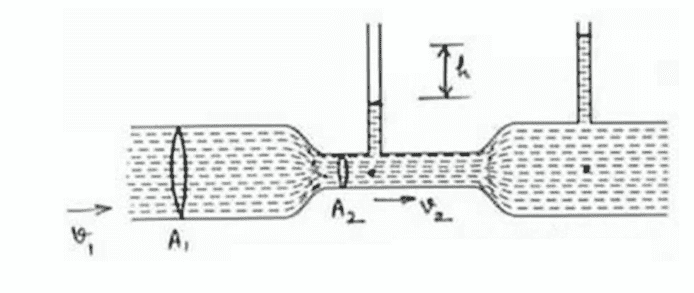
There is this pipe system of flowing ideal liquid. The cross-sections A1 and A2 are given, the water in the vertical pipes is static, and the height diffrence h is also given. I need to find the velecoties v1, v2.
The video with the problem and the answer:

In order to solve this, I need to use 3 equations:
1) A1*P1=A2*P2
2) 1/2*(v2)^2+P2=1/2*(v1)^2+P1
3) P2=P1+ρgh

I don't understand 3, because I thought the fact that the bottom of the left vertical pipe is lower than the right one matters. In other words, how can I claim that the pressure in the top of the water in left pipe equals to the point in the other pipe in the same height.

Thanks!

 

[scottdave]

If you measure down to the center of the pipe (where they are at the same vertical level), does that help?
Also, in the video they use P_a and P_b, where a is in the small section (where it is P2), and b is in the large section (which would be P1).
So really it should say:
P1=P2+ρgh because P1 (the pressure in the large section of pipe) is the higher pressure, it pushes the liquid higher up in the tube (higher from the same reference level).

 

[rude man]

Bernoulli applies to any streamline and we just pick the center line as our streamline.
A couple of points:
1. Just out of interest: you can't solve for p1 and p2 separately, just (p1 - p2), unless you know the levels in both pipes separately also.
2. Your 1st eq. is probably a typo.
3. Your eq. 2 needs the water density in it. Maybe another typo.
Scottdave has already pointed out the error in your eq. 3.
3.You can apply bernoulli to each pipe also, but it's a bit tricky: what is the effective v at the bottom of the pipes? Is it zero or is it v1 or v2 respectively? Again, think streamline: the obvious streamline is zero velocity thruout each pipe: once water is in each pipe there is no further flow of water from the conduits to the respective pipes, so no streamline there. Anyway, if you do you just get
p1 = p_atmosphere - ρgh₁, p2 = p_atmosphere - ρgh₂ and p1 - p2 = ρgh
which leads to the formula for v1 in the video.