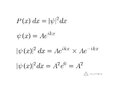Discussion Overview
The discussion revolves around the wave function for a free particle with a known momentum, specifically addressing the interpretation of the wave function given as Asin(kx) and its implications for probability density along the x-axis. Participants explore the mathematical properties of wave functions, normalization conditions, and the conceptual understanding of probability in quantum mechanics.
Discussion Character
- Technical explanation
- Conceptual clarification
- Debate/contested
Main Points Raised
- One participant questions how the probability can be constant if the square of the wave function Asin(kx) is not a constant.
- Another participant asserts that the correct wave function for a free particle is exp(i k x) and that the probability density is derived from the squared modulus of this complex function.
- Concerns are raised about the physical realizability of the wave function Asin(kx), with some participants stating it cannot be normalized.
- Discussion includes the distinction between a particle's position and the result of a measurement, with some participants suggesting that terminology reflects a deeper understanding of quantum mechanics.
- Participants discuss the implications of the modulus and modulus squared of the wave function, with some clarifying that a constant modulus does not represent a viable wave function.
- There is a mention of a later edition of the textbook that corrects previous misunderstandings regarding wave functions.
- Some participants express a need to understand complex conjugates and their role in the context of wave functions.
Areas of Agreement / Disagreement
Participants express disagreement regarding the correctness of the wave function presented in the textbook, with some asserting it is incorrect while others defend its interpretation. The discussion remains unresolved on whether the textbook's explanation is fundamentally flawed or if it is a matter of misinterpretation.
Contextual Notes
Participants highlight limitations in the textbook's treatment of wave functions, particularly regarding normalization and the distinction between probability distributions and measurement outcomes. There is also a recognition that the terminology used may affect understanding.
Who May Find This Useful
This discussion may be useful for students and enthusiasts of quantum mechanics seeking to understand wave functions, probability densities, and the nuances of quantum measurement theory.