Unknown's question at Yahoo Answers regarding the perimeter of a rectangle

[MarkFL]

Here is the question:

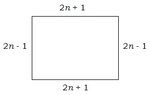
The dimensions of a rectangle are consecutive odd integers.

Find the smallest such rectangle with a perimeter of at least 35 cm.

Can you explain please.
It includes inequalities I think..

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Re: unknown's question at Yahoo! Answers regarding the perimeter of a rectangle

Hello unknown,

Let's let one pair of parallel sides, the smaller pair have length $2n-1$ and the other pair, the larger pair, have length $2n+1$, where $n$ is a natural number. We know they are both odd, because $2n$ must be even, and so adding/subtracting $1$ from an even number results in an odd number. We know they are consecutive odd numbers because their difference is $2$:

\(\displaystyle (2n+1)-(2n-1)=2n+1-2n+1=2\)

So, let's draw a diagram of our rectangle:

View attachment 1352

We see the perimeter $P$, which is the sum of the lengths of the four sides is:

\(\displaystyle P=(2n+1)+(2n-1)+(2n+1)+(2n-1)=8n\)

We are told that this perimeter must be at least 35 (measures in cm), so we may write:

\(\displaystyle 8n\ge35\)

Dividing through by $8$, we find:

\(\displaystyle n\ge\frac{35}{8}=4+\frac{3}{8}\)

Since $n$ is a natural number (a positive integer), we may then conclude we must have:

\(\displaystyle n=5\)

And so the two larger sides have length:

\(\displaystyle 2(5)+1=11\)

And the smaller sides have length:

\(\displaystyle 2(5)-1=9\)

This gives us a perimeter of $40\text{ cm}$. If we take the next smallest pair of consecutive integers, namely $7$ and $9$, we find the perimeter would be $32\text{ cm}$.