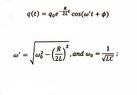hidemi
- 206
- 36
- Homework Statement
- An RLC circuit has a resistance of 200 Ω, an inductance of 15 mH, and a capacitance of 34nF. At time t = 0, the charge on the capacitor is 25
μC and there is no current flowing. After five complete cycles the energy stored in the capacitor is:
A) 0.64 μJ
B) 77 μJ
C) 0.49 mJ
D) 1.8 mJ
E) 9.2 mJ
The answer is A.
- Relevant Equations
- (see better expression below)
The equation is the only equation discussed in the textbook.
Is there a hint of how I could start this?
Is there a hint of how I could start this?