member 731016
- Homework Statement
- Please see below
- Relevant Equations
- E = hf
I am trying to find Planck's constant using Excel given the data:
I am using Linear regression and I have set the intercept to zero since photon energy is directly proportional to frequency from Planck's Law
My graph is,
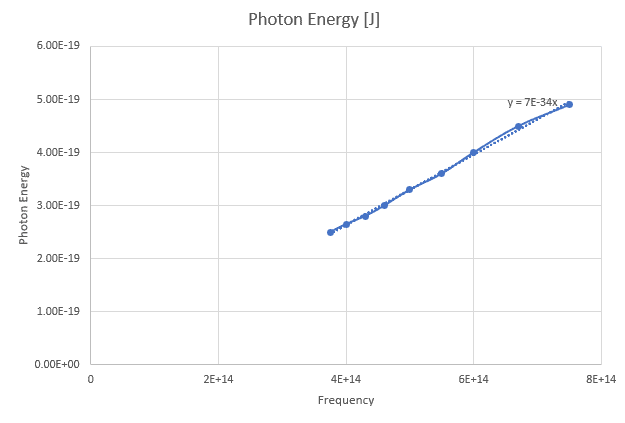
However, why is the linear regression giving an incorrect value for h? According to the data Planck's Constant is ##7 \times 10^{-34} Js ## but it meant to be ##6.63 \times 10^{-34} Js##
Many thanks!
| Frequency [Hz] | Photon Energy [J] |
7.5E+14 | 4.90E-19 |
6.7E+14 | 4.50E-19 |
6E+14 | 4.00E-19 |
5.5E+14 | 3.60E-19 |
5E+14 | 3.30E-19 |
4.6E+14 | 3.00E-19 |
4.3E+14 | 2.80E-19 |
4E+14 | 2.65E-19 |
3.75E+14 | 2.50E-19 |
My graph is,
However, why is the linear regression giving an incorrect value for h? According to the data Planck's Constant is ##7 \times 10^{-34} Js ## but it meant to be ##6.63 \times 10^{-34} Js##
Many thanks!