Using Bernoulli to find volume of water to pass through hole

[mm2424]

Homework Statement

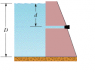
Consider the fresh water damn shown in the picture (attached below). The water behind the dam has depth D = 15 m. A horizontal pipe 4 cm in diameter passes through the dam at depth d = 6 m. A plug secures the opening. The plug is removed. Water water volume exits the pipe in 3 hours?

Homework Equations

p(atmosphere) + ρgh1 + 1/2ρ(v1)^2 = p(atmosphere) + ρgh2 + 1/2ρ(v2)^2

The Attempt at a Solution

I'm treating the left side of the equation as the water in the reservoir and the right hand of the equation as the water flowing through the hole.

I began by simplifying Bernoulli's equation, cancelling out the p(atmosphere) and the density of water. I also remove the 1/2(v1)^2 term, assuming v1 is very small:

gh1 = gh2 + 1/2(v2)^2

I start to get confused in terms of the heights I should be using here.

Is h1 the full height of the water (15 m)? The answer key in my book seems to treat h1 as the full height of the water (15 m), but that confuses me, since it seems like the center of mass of the water would only be 7.5 m up.

I assume h2 is the height of the water in the pipe, which is about 9 m (15 m - 6 m).

I'm confused because if I trust my reasoning and use the center of mass of the water, v2 is negative, which of course makes no sense.

Am I missing something here? Is there some reason why I should consider h1 to be 15 m, despite the fact that most of the water isn't really 15 m up?

Thanks!

(ps, v2 is supposed to be 10.84 m/s^s, making the final answer 147 m^3.

 

[LawrenceC]

In using Bernoulli's equation, place position 1 at the water surface where the height is considered d as shown in your picture. Choose position 2 at the outlet with the height being zero. In the end you subtract the water heights when you solve for V2.

Or you can choose h1 as D then follow up by choosing h2 as D-d. When you move the D-d to the left hand side of the equation, D cancels out and you're left with d as above.

Your choice of zero for the velocity (V1) at the free surface is correct.

 

[mm2424]

I see, so then it is ok to ignore the water below the pipe, since we're setting the pipe's height to be 0. However, should we still consider the height of the water outside the pipe as being d and not d/2? Why don't we need to consider the center of the mass of the water? It seems like using a height of d assumes that all of the water is at height d, whereas the center of mass is lower. Granted, I could be really messing this up...

 

[LawrenceC]

It is a reservoir. One must assume the level does not drop. The height is d, not d/2. Pessure is density times depth. The pressure difference is what causes the fluid to move.