BunDa4Th
- 188
- 0
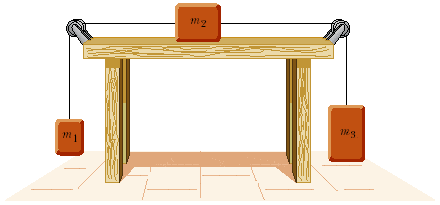
Three objects with masses m1 = 4.0 kg, m2 = 10.0 kg, and m3 = 15.0 kg, respectively, are attached by strings over frictionless pulleys, as indicated in Figure P5.32. The horizontal surface is frictionless and the system is released from rest. Using energy concepts, find the speed of m3 after it moves down a distance of 2.5 m.
Okay, I am lost at this. At first I thought this was a simple problem using
V^2 = 2adeltaX which apparently is not, if it is then i am doing something wrong. I read on the conservative energy in the book I am using and understand a bit of it but not sure where to start.
I seriously don't know where to start or what i am doing right now. I seem to enter number randomly sometimes.
Okay, I am lost at this. At first I thought this was a simple problem using
V^2 = 2adeltaX which apparently is not, if it is then i am doing something wrong. I read on the conservative energy in the book I am using and understand a bit of it but not sure where to start.
I seriously don't know where to start or what i am doing right now. I seem to enter number randomly sometimes.
Last edited by a moderator: