Using Small Examples to Solve Combinatorial Problems

  • Context: High School 
  • Thread starter Thread starter sahilmm15
  • Start date Start date
  • Tags Tags
    Exponents
Join the discussion
Ask a follow-up here, or get your own question answered by working scientists, mathematicians and engineers — people, not an autocomplete.
Real named experts · corrections over time · the nuance an AI answer skips
Sign up Log in
6 replies · 1K views
sahilmm15
Messages
100
Reaction score
27
In the below picture I understood the problem and also understood the solution. But I am not clear on why did they choose this particular method. So my question is why did they divided 50 with powers of 2 and 3, and what relation does ##50## have with ##50!## ( I am clear on the solution part but I am clueless how would have the author thought of the problem.) Thanks!
IMG_20201224_143619.jpg
 
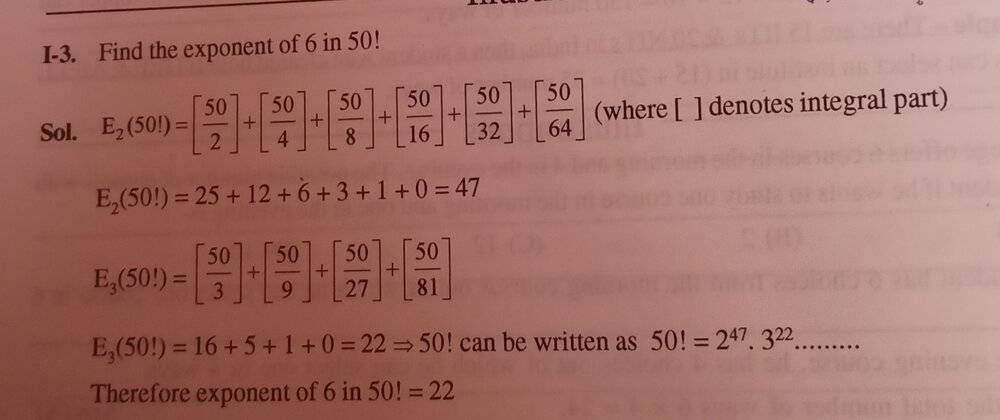
Last edited by a moderator:
Physics news on Phys.org
PeroK said:
It's just counting factors isn't it? It's not clear how much you understand.
I think I overcomplicated it. Can you explain me from scratch.
 
sahilmm15 said:
I think I overcomplicated it. Can you explain me from scratch.
If you look at ##10!## say, then count the factors of ##2##. We have:

2, 4, 6, 8 and 10 all have a factor of 2 (that's five factors of 2)

4 and 8 have a second factor of 2 (that's two more factors of 2)

8 has a third factor of 2 (that's another one)

Altogether, therefore, ##10!## has eight factors of 2. And doing this for the other primes we see that: $$10! = 2^8 \times 3^4 \times 5^2 \times 7$$
 
  • Like
Likes   Reactions: sahilmm15
PeroK said:
If you look at ##10!## say, then count the factors of ##2##. We have:

2, 4, 6, 8 and 10 all have a factor of 2 (that's five factors of 2)

4 and 8 have a second factor of 2 (that's two more factors of 2)

8 has a third factor of 2 (that's another one)

Altogether, therefore, ##10!## has eight factors of 2. And doing this for the other primes we see that: $$10! = 2^8 \times 3^4 \times 5^2 \times 7$$
This was so simple. Thanks!
 
PeroK said:
If you look at ##10!## say, then count the factors of ##2##. We have:

2, 4, 6, 8 and 10 all have a factor of 2 (that's five factors of 2)

4 and 8 have a second factor of 2 (that's two more factors of 2)

8 has a third factor of 2 (that's another one)

Altogether, therefore, ##10!## has eight factors of 2. And doing this for the other primes we see that: $$10! = 2^8 \times 3^4 \times 5^2 \times 7$$
What I learned from this example is if you cannot comprehend a bigger problem take a smaller example and relate to the steps. I saw you doing this from past 2 answers and it worked beautifully.
 
  • Like
Likes   Reactions: PeroK
sahilmm15 said:
What I learned from this example is if you cannot comprehend a bigger problem take a smaller example and relate to the steps. I saw you doing this from past 2 answers and it worked beautifully.
Especially for these combinatorial problems. If in doubt, count for a low-value example. Often that's how you see what's going.

And, it gives you an answer to check against any general formula you come up with.
 
  • Informative
Likes   Reactions: sahilmm15