Using the given information , find the value of x

In summary, the given information provides necessary data or facts to solve for the value of x. This can be achieved by using algebraic equations, creating a graph or table, or following general steps such as identifying known values and unknown variables, setting up equations, and solving them. Multiple pieces of given information may be needed to find the value of x, and if the given information is insufficient, assumptions or estimates may be necessary to find an approximate solution. Careful checking for errors or missing data is also important in solving for x.
  • #1
mathlearn
331
0
View attachment 6007

What I know,

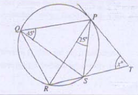
$\angle RQS=25^\circ$(Inscribed angle theorem) & $\angle RSP=110^\circ$(opposite angles of a cyclic quadrilateral add upto 180)

$\angle TSP=70^\circ$(angles on a straight line add upto 180)

(Happy) Many Thanks
 

Attachments

  • Capture.PNG
    Capture.PNG
    12.2 KB · Views: 71
Last edited:
Mathematics news on Phys.org
  • #2
mathlearn said:
What I know,

$\angle RQS=25^\circ$(Inscribed angle theorem) & $\angle RSP=110^\circ$(opposite angles of a cyclic quadrilateral add upto 180)

$\angle TSP=70^\circ$(angles on a straight line add upto 180)

(Happy) Many Thanks
Hint: Note that $\angle TPS=\angle PQS$.
 
  • #3
caffeinemachine said:
Hint: Note that $\angle TPS=\angle PQS$.

Many Thanks (Sun)
 

FAQ: Using the given information , find the value of x

What is the given information?

The given information refers to any relevant data or facts that are provided in order to solve for the value of x. This could include equations, measurements, or other known values.

How do I use the given information to find the value of x?

The given information can be used in a variety of ways, depending on the specific problem. In many cases, algebraic equations can be set up using the given information and then solved for x. Alternatively, the given information may be used to create a graph or table to visually represent the relationship between x and the other variables.

What steps should I take to solve for x?

The steps to solve for x will vary depending on the given information and the specific problem. However, some general steps may include: identifying the known values and unknown variable, setting up an equation or system of equations, solving the equations using algebraic techniques, and checking the solution to ensure it is valid.

Can I use multiple pieces of given information to find the value of x?

Yes, it is often necessary to use multiple pieces of given information in order to find the value of x. This could involve using multiple equations, combining equations, or using multiple data points to create a graph or table.

What should I do if the given information is insufficient to solve for x?

If the given information is insufficient, it may not be possible to find the exact value of x. In this case, it may be necessary to make assumptions or estimates in order to find an approximate solution. It is also important to check the given information for any errors or missing data that could be preventing a solution.

Similar threads

MHB Finding all Possible Values of $x$ in Triangle ABC
Replies
1
Views
995
MHB Physics-Using vectors to find the components
Replies
1
Views
2K
MHB Find the angle X inside a pentagon with a square
Replies
4
Views
3K
MHB Find unknown angles of a triangle
Replies
6
Views
3K
MHB Λ and μ are scalars, find the value of λ and the value of μ
Replies
4
Views
2K
MHB Where Did I Go Wrong in Calculating the Value of x in These Triangle Problems?
Replies
4
Views
2K
MHB Find value of x and area of parallelogram: a,b,c,P
Replies
2
Views
2K
MHB Given value of cos(A) and quadrant of A, find sin(A) and tan(A)
Replies
2
Views
2K
MHB Finding exact 3d coordinates in a falling pipe system with corners
Replies
20
Views
4K
MHB Finding distances to the frisbee
Replies
3
Views
3K

Hot Threads

Recent Insights

Back
Top