SUMMARY
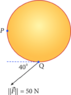
The discussion focuses on calculating the torque applied to a disk when a force of 50N is exerted at point Q, located at the bottom of the disk with a radius of 8m. The angle between the force vector and the vector from point P to Q was initially miscalculated as 85 degrees but was corrected to 95 degrees. The torque magnitude is determined using the equation |T| = |F|sin(Theta)*|r|, where the correct values are substituted to find the torque.
PREREQUISITES
- Understanding of vector mathematics and torque calculations
- Familiarity with the cross product of vectors
- Knowledge of trigonometric functions and their applications in physics
- Ability to interpret and manipulate coordinate systems in three dimensions
NEXT STEPS
- Study the properties of the cross product in vector calculus
- Learn about torque in rotational dynamics and its applications
- Explore the use of trigonometric identities in physics problems
- Practice solving similar problems involving forces and torques on rigid bodies
USEFUL FOR
Students studying physics, particularly those focusing on mechanics and torque calculations, as well as educators seeking to clarify concepts related to forces and rotational motion.