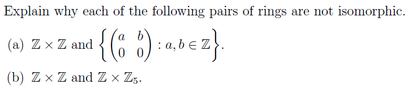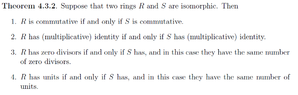Verifying Answers to "Zero Divisors & Isomorphism Theorem"

[Joe20]

I have gotten the following answer to (a) and (b) which require verification on them. I have also attached the theorem for reference.

(a) Z x Z => have zero divisors
The matrix has no zero divisors (no nonzero matrix when multiplied to the matrix gives zero element)
Hence not isomorphic. (b) Z x Z => have 2 elements
Z x Z subscript 5 => have 5 elements ( [0,0] [0,1] [0,2] [0,3] [0,4] )
Hence not isomorphic.

 

[Euge]

Your reasoning for part (a) is incorrect since $\begin{pmatrix}0&1\\0&0\end{pmatrix}$ is a zero divisor: $\begin{pmatrix}0&1\\0&0\end{pmatrix}\begin{pmatrix}1&1\\0&0\end{pmatrix} = \begin{pmatrix}0&0\\0&0\end{pmatrix}$ Also, your reasoning for (b) is incorrect: both $\Bbb Z\times \Bbb Z$ and $\Bbb Z \times \Bbb Z_5$ are infinite rings.

 

[Joe20]

Your reasoning for part (a) is incorrect since $\begin{pmatrix}0&1\\0&0\end{pmatrix}$ is a zero divisor: $\begin{pmatrix}0&1\\0&0\end{pmatrix}\begin{pmatrix}1&1\\0&0\end{pmatrix} = \begin{pmatrix}0&0\\0&0\end{pmatrix}$ Also, your reasoning for (b) is incorrect: both $\Bbb Z\times \Bbb Z$ and $\Bbb Z \times \Bbb Z_5$ are infinite rings.

So how do I go about approaching these two questions? I have no clue.

 

[I like Serena]

So how do I go about approaching these two questions? I have no clue.

For (a), let's start with the first property.
Are they both commutative?
What do we get for (a,b)x(c,d) and (c,d)x(a,b) in both cases?

For (b), which units do they have?

 

[Joe20]

I have done up part (a), hence need verification on that as attached.

Next for part (b), I am not sure how to identify the unit(s) from Z x Z and Z x Z subscript 5. May need someone's help.

Thanks.

 

[Euge]

I have done up part (a), hence need verification on that as attached.

Next for part (b), I am not sure how to identify the unit(s) from Z x Z and Z x Z subscript 5. May need someone's help.

Thanks.

First consider $\Bbb Z$ and $\Bbb Z_5$. The units in $\Bbb Z$ are $\pm 1$ and the units of $\Bbb Z_5$ are the nonzero elements of $\Bbb Z_5$. Next, consider the fact that if $R$ and $S$ are rings with unity, then the units of $R\times S$ are of the form $(u,v)$ where $u$ is a unit in $R$ and $v$ is a unit in $S$.

 

[Joe20]

for part b, i have gotten the units for Z x Z as (1,1) , (1,-1) , (-1,1) , (-1, -1) and units for Z x Z subscript 5 as (1, 1), (1,2), (1,3) , (1,4), (-1,1), (-1,2), (-1,3), (-1,4).

hence would require someone to verify the results stated. Thanks

 

[Euge]

for part b, i have gotten the units for Z x Z as (1,1) , (1,-1) , (-1,1) , (-1, -1) and units for Z x Z subscript 5 as (1, 1), (1,2), (1,3) , (1,4), (-1,1), (-1,2), (-1,3), (-1,4).

hence would require someone to verify the results stated. Thanks

It's correct.