sfensphan
- 9
- 1
The setup: I have a mass (m1)connected to a much, much larger mass (m2) via a preloaded spring. They start out in contact because the preloaded spring holds them together. Now suppose the large mass is subject to vibrations, possibly at the resonance of the structure. Will the two masses separate? If they do, what is the maximum distance between the two?
Will the two masses separate?
My original chain of thought was that if the spring force is less than the inertial force of the small mass, then the two will separate.
F_spring = -k(Δx)
k = spring constant
Δx = displacement from spring resting state. Since there is a preload, this is non-zero
F_inertia = m1 * a
m1 = mass of the small mass
a = acceleration. This should be sinusoidal, since it's a vibration
I would then compare the two and see which one is larger. I would use the max value of F_inertia during this comparison.
If they do, what is the maximum distance between the two?
This is where I get a little lost. A static calculation would be to find where Δx is such that F_spring = F_inertia.
But what if the system vibrated at resonance frequency (which I believe would be sqrt(k/m1) for this case)?
How do I deal with the preload?
Is the Force body diagram such that the sinusoidal force acts directly on the m1?
Do I need to know how much the larger mass is displaced?
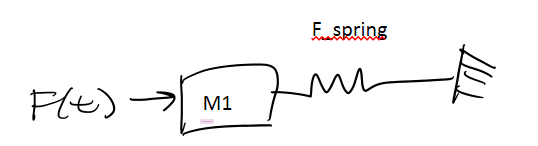
Will the two masses separate?
My original chain of thought was that if the spring force is less than the inertial force of the small mass, then the two will separate.
F_spring = -k(Δx)
k = spring constant
Δx = displacement from spring resting state. Since there is a preload, this is non-zero
F_inertia = m1 * a
m1 = mass of the small mass
a = acceleration. This should be sinusoidal, since it's a vibration
I would then compare the two and see which one is larger. I would use the max value of F_inertia during this comparison.
If they do, what is the maximum distance between the two?
This is where I get a little lost. A static calculation would be to find where Δx is such that F_spring = F_inertia.
But what if the system vibrated at resonance frequency (which I believe would be sqrt(k/m1) for this case)?
How do I deal with the preload?
Is the Force body diagram such that the sinusoidal force acts directly on the m1?
Do I need to know how much the larger mass is displaced?