bikramjit das
- 12
- 0
vibration problem!
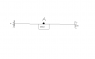
Question:There is a fixed end beam PQ. It is carrying a motor M. The motor is unbalanced and when the motor is rotating ,it is making the beam to vibrate with a frequency equal to the speed of the motor. A small mass is kept at point A just above the motor on the beam. it also goes up & down along with the beam . When the motor speed is 120 - 150rpm, the object at A is loosing contact with the beam & is actually dancing on the beam. Determine the amplitude of vibration when the speed of motor is 120 rpm and when 150 rpm . Then calculate the natural frequency of the system.
|---------------------M--------------------|
data may be suitably assumed.
can't get any of them
This is a base excitation problem. but the natural frequency is diff. to find. pls help
Homework Statement
Question:There is a fixed end beam PQ. It is carrying a motor M. The motor is unbalanced and when the motor is rotating ,it is making the beam to vibrate with a frequency equal to the speed of the motor. A small mass is kept at point A just above the motor on the beam. it also goes up & down along with the beam . When the motor speed is 120 - 150rpm, the object at A is loosing contact with the beam & is actually dancing on the beam. Determine the amplitude of vibration when the speed of motor is 120 rpm and when 150 rpm . Then calculate the natural frequency of the system.
|---------------------M--------------------|
data may be suitably assumed.
Homework Equations
can't get any of them
The Attempt at a Solution
This is a base excitation problem. but the natural frequency is diff. to find. pls help
Attachments
Last edited: