Visualizing Series Bandpass Filters: A Graphical Approach

[so_gr_lo]

Homework Statement

I am plotting Vout/Vin against frequency for a RLC series bandpass filter, where Vout is across the resistor. The resulting graph has max Vout/Vin of about 1.5, the max is supposed to be 1 in a bandpass filter. The Vout/Vin values are experimental, could a max Vout/Vin of 1.5 occur in an experiment? And what could be the reason for this?

Relevant Equations

Vin/Vout = R / (R+wL -1/wc) , where w = omega

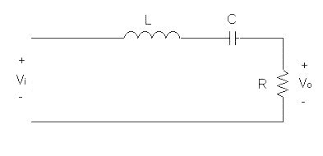
this is the circuit

this is the theoretical graph

 

[BvU]

Hi,

Your relevant equation is an equation with complex quantities on both sides.
(I think you switched in and out subscripts ?)

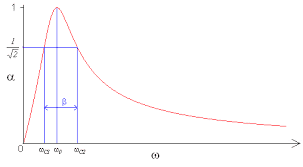
What you measure is most likely the real ratio of two amplitudes. As plotted in the theoretical graph.
For the complex impedance of the RLC series we have $$Z^2 = R^2 + \left (\omega L - {1\over \omega C}\right )^2 $$ with a minimum $Z=R$ (and $V_{out}/V_{in}=1$ ).

A measured ratio can deviate if the measurement equipment influences the circuit. So you have to check values of components and equipment.

$\$

 

[so_gr_lo]

So what equation could you use to plot theoretical values of Vout / Vin ?

 

[DaveE]

So what equation could you use to plot theoretical values of Vout / Vin ?

Are you familiar with complex number arithmetic? With the representation of impedance using complex numbers? I think that is necessary to understand this without a tremendous amount of work.

Do you know about simple circuit analysis, like voltage dividers?

This is important information for us to know to help appropriately.

 

[DaveE]

Khan Academy has some really good tutorials on these subjects.