Finding R and C values for an active second-order bandpass filter

[palacetrading]

I have been assigned the task to design an active bandpass filter with a passband of 0.1 to 10 Hz. At these two frequencies, there should be an attenuation of -6dB or more. So far I have selected my circuit layout which can be seen below

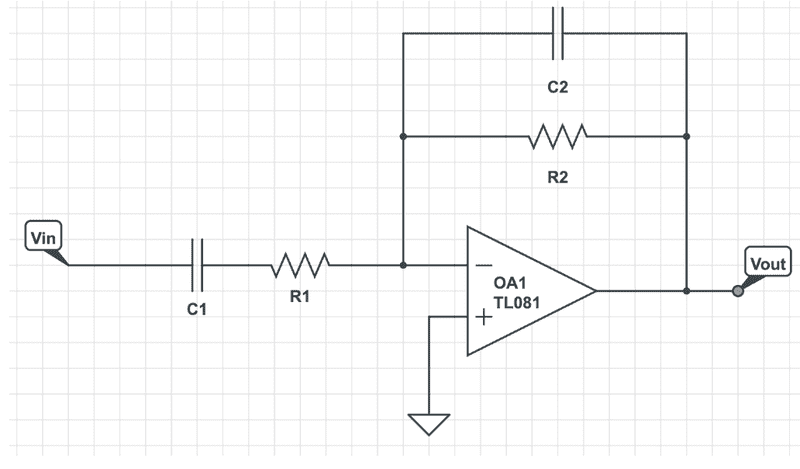
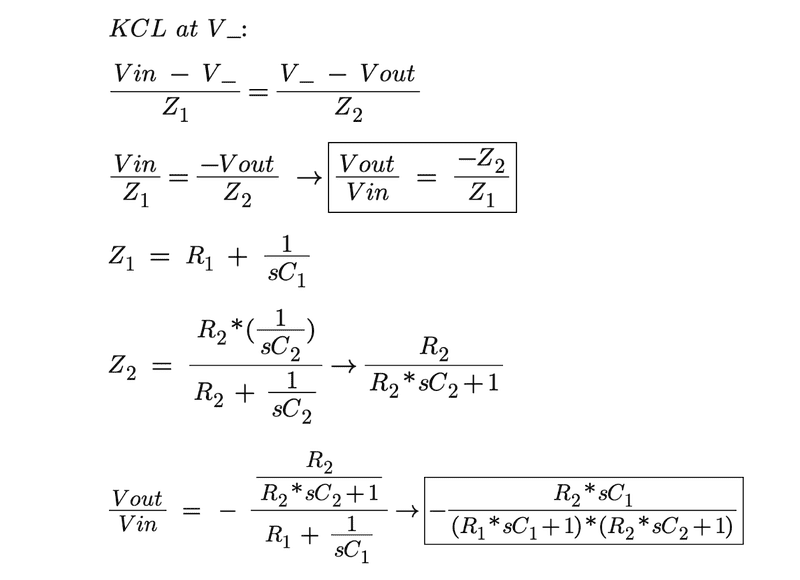
I found my transfer function so that I could calculate the R and C values and then converted into jw form. From here, I used math to remove the imaginary numbers and now I have my transfer function in terms of w and the components.

My questions are as follows:
1. Is the w that I need to plug in the center frequency? So sqrt(0.1*10) = 1 Hz or would it be 1*2pi?
2. Have I set up my transfer function correctly for finding when 0.1 and 10 Hz will be -6db by setting it equal to 0.5?
3. If the above are true, in theory, do I just start plugging in values for the components to make the equation equal 0.5?

 

[hutchphd]

The ω in the formulas should be in natural units (rad/s) but get the conversion correct $$1Hz=2\pi (rad/s)$$ The rest is probably good (I'm not going to check your arithmetic.......)

 

[gneill]

I think your H(s) mixed up the numerator's R term. You wrote:

R₁ should be R₂.

 

[palacetrading]

You are correct, thanks. Do you know the answer to any my questions from the original post?

I think your H(s) mixed up the numerator's R term. You wrote:
View attachment 322719

View attachment 322720

R₁ should be R₂.

 

[palacetrading]

The ω in the formulas should be in natural units (rad/s) but get the conversion correct $$1Hz=2\pi (rad/s)$$ The rest is probably good (I'm not going to check your arithmetic.......)

Yes, the conversion is 2pi*f to get to radians. My arithmetic is correct, what I am not sure about is finding the corner frequencies to have -6db attenutation.

 

[DaveE]

Great work so far, you've done the hard part, I think. Now we just have to think a bit about the equations you have. I would continue the algebra a bit more to get this transfer function into the canonical factored pole zero form (although you're already mostly there), this will make the interpretation much easier for you.

$$ H(s) = -\frac{R_2sC1}{(R_1C_1s+1)(R_2C_2s+1)} = -(\frac{R_2}{R_1}) \frac{1}{(1+\frac{1}{R_1C_1s})(1+R_2C_2s)} = -(\frac{R_2}{R_1}) \frac{1}{(1+\frac{\omega_1}{s})(1+\frac{s}{\omega_2})} $$

Where $\omega_1 \equiv \frac{1}{R_1C_1}$ , $\omega_2 \equiv \frac{1}{R_2C_2}$, and $s \equiv j\omega \equiv j2\pi f$. Then $\omega_1$ and $\omega_2$ are the key frequency dependent parameters, the poles and zeros of the transfer function.

Now notice that when $\omega \gg \omega_1$ then $(1+\frac{\omega_1}{s}) \approx 1$ .
Also, when $\omega \ll \omega_2$ then $(1+\frac{s}{\omega_2}) \approx 1$ .

For a BPF with a wide passband, we can assume both $\omega \gg \omega_1$ and $\omega \ll \omega_2$ at the center frequency of the filter (normally, the geometric mean of the nearest higher and lower frequency poles/zeros; $\omega_o = \sqrt{\omega_1 \omega_2}$). Then $H(s) \approx -(\frac{R_2}{R_1})$ . This we would call the midband or passband gain. This is often the value that the attenuation is referred to in filters, but that's not universally true. The question "attenuation compared to what?" may be necessary.

From this midband point if you decrease the frequency you really only need to care about $\omega_1$ since the approximation $\omega \gg \omega_1$ will fail. In that region we can approximate $H(s) \approx -(\frac{R_2}{R_1}) \frac{1}{(1+\frac{\omega_1}{s})}$. You will want to choose the value of $\omega_1$ so that $|\frac{1}{(1+\frac{\omega_1}{s})}| = 1/2$ according to your requirements.

You should be able to continue from here for the rest of the problem. Note that we have made some approximations that you may need to verify are acceptable with your specific parameters.

PS: These, and similar, approximations are the basis for the asymptotes of bode plots. You'll want to think about these plots whenever you are working with this kind of problem. When you are proficient with this you will be able to quickly sketch the transfer function desired and immediately translate that into the transfer function equation by identifying the salient gains and "corner frequencies" where the filter behavior changes, where your approximations shift, as we did above.

 

[DaveE]

Totally nitpicking... But I would call this a first order BPF.

 

[palacetrading]

Totally nitpicking... But I would call this a first order BPF.

Okay. I was going based off the definition of the filter I am using from this website. https://www.electrical4u.com/band-pass-filter/

 

[palacetrading]

Great work so far, you've done the hard part, I think. Now we just have to think a bit about the equations you have. I would continue the algebra a bit more to get this transfer function into the canonical factored pole zero form (although you're already mostly there), this will make the interpretation much easier for you.

Dave, thanks for the response. I was following until the point where you started talking about the midband.

I was able to find some values that worked to create the filter shape that I need:
R1 = 100e3; R2 = 100e3; C1 = 9.2e-6; C2 = 275e-9;

They produce this bode plot

I was able to figure out how to calculate the high pass filter values (see my math below) but am running into issues with solving for the low pass ones.

Please let me know how to proceed from here.

 

[DaveE]

Um... OK, I'm pretty confused here. I guess you've redefined H(s) now as the voltage divider for $V_x$. Best to use a different name for that, like G(s). Anyway, I don't know why you care about $V_x$. You did an excellent job before of developing the filter transfer function, so the math part was pretty much done. I'm not sure why you are doing something different now.

 

[The Electrician]

Totally nitpicking... But I would call this a first order BPF.

A little more than halfway down the page here: https://www.electrical4u.com/band-pass-filter/
we find this heading:

First Order Band Pass Filter Transfer Function​

And right after that we find: "A first order band pass filter is not possible, because it has minimum two energy saving elements (capacitor or inductor)."

 

[The Electrician]

Dave, thanks for the response. I was following until the point where you started talking about the midband.

I was able to find some values that worked to create the filter shape that I need:
R1 = 100e3; R2 = 100e3; C1 = 9.2e-6; C2 = 275e-9;

They produce this bode plot
View attachment 322752

I was able to figure out how to calculate the high pass filter values (see my math below) but am running into issues with solving for the low pass ones.

View attachment 322753View attachment 322754

Please let me know how to proceed from here.

Your result is very close to the exact result.

To get the exact result you must solve two simultaneous equations for C1 and C2. You need to have an expression for the magnitude of your transfer equation and set it equal to 1/2 at the two cutoff frequencies (.1 and 10). This will give you the two equations.

One problem with doing this is that your expression for |H(jw)| in post #1 is incorrect. You'll need to research the correct way to form that expression. Hint: it involves the complex conjugate.

 

[LvW]

A little more than halfway down the page here: https://www.electrical4u.com/band-pass-filter/
we find this heading:

First Order Band Pass Filter Transfer Function​

And right after that we find: "A first order band pass filter is not possible, because it has minimum two energy saving elements (capacitor or inductor)."

As far as I know the order of any filter is determined by the order of the transfer functions denomionator.
As a consequence, a 1st-order bandpass does not exist. This view follows also from the properties of the lowpass-bandpass transformation.
Using this transformation, 2nd-oder lowpass results always in a 4th-order bandpass - hence, a 1st-order lowpass (smallest order) gives a 2nd-order bandpass.

 

[DaveE]

As far as I know the order of any filter is determined by the order of the transfer functions denomionator.
As a consequence, a 1st-order bandpass does not exist. This view follows also from the properties of the lowpass-bandpass transformation.
Using this transformation, 2nd-oder lowpass results always in a 4th-order bandpass - hence, a 1st-order lowpass (smallest order) gives a 2nd-order bandpass.

Yes, I totally agree about the order of the transfer function. Perhaps it's my own quirk, but since a BPF with one pole can't exist, my assumption is that "first order BPF" means two poles. But, this really doesn't make sense in general because what about a BPF with three poles, doesn't that have to be 3rd order? Then what happened to the two pole version? I guess I skip over those? IDK.

These names don't really matter much in practice. Anyone designing filters is working almost entirely with the transfer function, bode plots, schematics, etc. the words don't get used, or are used in context like "4th order Chebyshev" etc.

PS: BTW, you will sometimes hear people say "symmetric 2nd order BPF". That one would have 4 poles.

 

[The Electrician]

palacetrading, have you had any luck deriving the correct expression for |H(jw)|?

 

[DaveE]

One problem with doing this is that your expression for |H(jw)| in post #1 is incorrect. You'll need to research the correct way to form that expression. Hint: it involves the complex conjugate.

It looks OK to me. The line before is just wrong, or maybe it's just a typo with the j's left in place. IDK, I'm not sure what "→" means there.

 

[The Electrician]

It looks OK to me. The line before is just wrong, or maybe it's just a typo with the j's left in place. IDK, I'm not sure what "→" means there.

He simplified things in a different way than I did and didn't show enough intermediate steps for me to follow his work. When I want to compare two algebraic expressions that may have been simplified to an apparently different result, I evaluate them numerically with random values. Because palacetrading interchanged R1 and R2 in the numerator of his final result, my test using random inputs gave a different result comparing what his expression evaluated to and what mine did. I see now that gneill pointed this out, which I did not notice. Using the values palacetrading found, his result and my result evaluate to the same value because R1 and R2 are both the same value, 100k, which might lead one to think his result was totally correct, which it is not unless the R1/R2 interchange is fixed.

Now all he has to do is fix the R1/R2 mixup in his expression and set up two simultaneous equations and get the desired C1 and C2 values. I see that he hasn't been here lately; we may have seen the last of him.