EmilyRuck
- 134
- 6
Hello!
This is the first time I write in the forum. I hope to be fully in-topic.
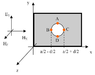
I'm dealing with a rectangular waveguide discontinuity: a perfect-conductor plane orthogonal to the propagation direction, with a circular aperture in the centre of the guide section. The structure is symmetrical along the x-axis and the y-axis and I drew it in the attachment, where the z axis is outgoing from the screen.
In my note the professor talked about a strange "Edge Theorem" (which we didn't demonstrate and which I can't find in any book). The Theorem says that:
- a field component which is parallel to an edge is diffracted but not folded (and so it doesn't generate any new field component);
- a field component which is orthogonal to an edge is diffracted and folded along the plane perpendicular to the edge (so it could generate a new field component).
The discontinuity is reached by the fundamental TE10 mode: in my coordinate system, it has EY, HX and HZ field components.
According to the Theorem, when EY reaches the upper and the lower part of the circle (points A and D in the picture) it is orthogonal to the circle edge and it generates an EZ component.
When HZ reaches the left and the right part of the circle (points B and C in the picture) it generates HX; similarly, in those points HX generates HZ.
But what about HY and EX? I can't see how they are generated, but they are, because I wrote in my notes that the field becomes a 6-components field.
The only electric field component is EY, but when it reaches the oblique edge between A and B, it generates an EZ again and not an EY! What is wrong?
Thank you anyway!
Bye,
Emily
This is the first time I write in the forum. I hope to be fully in-topic.
I'm dealing with a rectangular waveguide discontinuity: a perfect-conductor plane orthogonal to the propagation direction, with a circular aperture in the centre of the guide section. The structure is symmetrical along the x-axis and the y-axis and I drew it in the attachment, where the z axis is outgoing from the screen.
In my note the professor talked about a strange "Edge Theorem" (which we didn't demonstrate and which I can't find in any book). The Theorem says that:
- a field component which is parallel to an edge is diffracted but not folded (and so it doesn't generate any new field component);
- a field component which is orthogonal to an edge is diffracted and folded along the plane perpendicular to the edge (so it could generate a new field component).
The discontinuity is reached by the fundamental TE10 mode: in my coordinate system, it has EY, HX and HZ field components.
According to the Theorem, when EY reaches the upper and the lower part of the circle (points A and D in the picture) it is orthogonal to the circle edge and it generates an EZ component.
When HZ reaches the left and the right part of the circle (points B and C in the picture) it generates HX; similarly, in those points HX generates HZ.
But what about HY and EX? I can't see how they are generated, but they are, because I wrote in my notes that the field becomes a 6-components field.
The only electric field component is EY, but when it reaches the oblique edge between A and B, it generates an EZ again and not an EY! What is wrong?
Thank you anyway!
Bye,
Emily