Wavelet transform (CWT and DWT)

[fog37]

Hello,
I recently got interested in wavelets. The main idea seems clear: we compute the inner product between the signal $x(t)$ and a chosen wavelet for different scale factors and translations of the wavelet over the signal. The inner product provides the coefficient for a wavelet with a specific scale factor $a$, which is inversely related to the wavelet frequency $f$, as we translated the wavelet over $x(t)$.

Apparently, given a discrete signal $x(t)$, we can calculate either its continuous wavelet transform CWT and its discrete wavelet transform (DWT). Both are transforms are discrete in the sense that the scale parameter and translation parameter have a finite numbers of values...

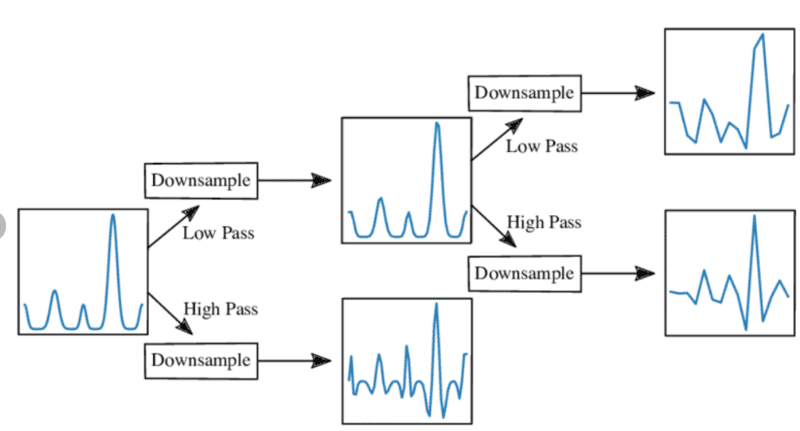
My question: the DWT can be represented as a bank of low-pass and high-pass filters. We send the signal $x(t)$ into the first pair of filter and then pass its downsampled low-pass versions into subsequent filter pairs This process apparently produces approximation and detail coefficients...I am not clear on this process...What do we do with the approximation and detail coefficients? Is the signal decomposed into a weighted sum of wavelet functions plus a weighted sum of scaling functions?

We end up with a single downsampled low-pass version of the input signal and two downsampled high-pass versions....How does that relate to obtaining a spectrogram $F(\omega, t)$ of the input signal $x(t)$?

Thank you!

 

[osilmag]

If I'm not mistaken, the coefficients are displayed over a set band of frequencies (the wavelet). Whereas, Fourier displays the amplitude of the entire spectrum of frequencies. So, your spectrogram would be limited by the wavelet.

 

[fog37]

If I'm not mistaken, the coefficients are displayed over a set band of frequencies (the wavelet). Whereas, Fourier displays the amplitude of the entire spectrum of frequencies. So, your spectrogram would be limited by the wavelet.

My understanding is that the detail and approximation coefficients will be the coefficients which will multiply the scaling (father) wavelets and the mother wavelets. The filters above are all bandpass filters with different frequency ranges....

I am not sure why the CWT, which is also discrete in the scale parameter $a$ and translation parameter $\tau$, does not need the father wavelet....Any idea?

 

[osilmag]

I guess I would say that once you have down or up sampled the signal, you have moved on to a different wavelet, with different a and t values. I would agree with you that it is a weighted sum of wavelet functions with their scalar coefficient.

 

[fog37]

I guess I would say that once you have down or up sampled the signal, you have moved on to a different wavelet, with different a and t values. I would agree with you that it is a weighted sum of wavelet functions with their scalar coefficient.

Thank you!

And what is your intuition about the filters corresponding to scaled and shifted mother wavelets?
How do you factor in the father wavelet (scaling function) which is not present in the CWT that is only based on assembling the signal as a superposition of scaled and shifted mother wavelets (the daughter wavelets)?