We must show that any point of this segment....

[frostysh]

(mentor note: moved post from non-homework forum, hence no template)

The problem: We have a segment of the line, the endpoint of which is stocked to the Axes, different endpoints, to the different axes. This segment is moving. We must show that any point of this segment will have ellipse-like trajectory, for an exception for the center point and endpoints. - I hope you will understand it, because I am to lazy and sleepy to draw a GIF-animation of the motion.

So I have mind activity for a while...

And I have draw a lot graphs on ma paper stuff for the special case - Isosceles right triangle position of the line-segment, and I have draw a many kind of trajectories there, so I have decided to try the ellipse-like trajectories in the center of origin of Coords. And then I have start to check this trajectories.

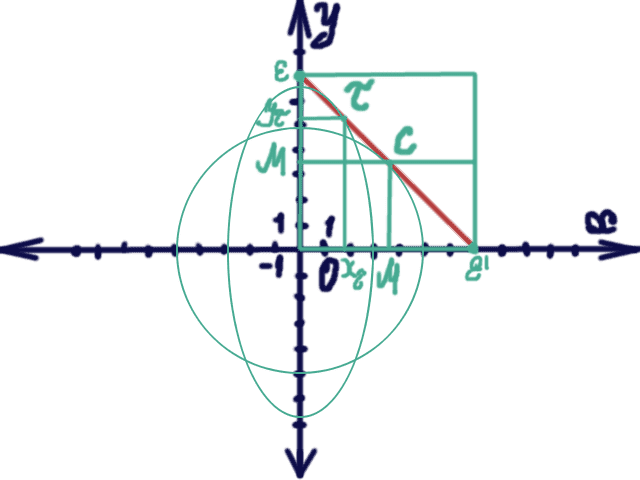
For the first, for the Center point, which is C on the graph stuff. I have remembered Pythagorean stuff in the case of Isosceles right triangle,

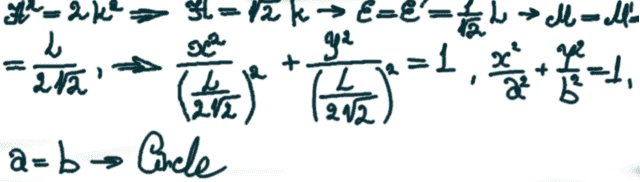
Also I have remembered something about Thales' theorem, and stuff about equal segments of the angle sides, so I have found M and M' points. This points will be semi-self-axis in our guessed Ellipse, so they will be equal, if they equal our Ellipse, will be something like Circle. I have decided to invoke the same trick for the point tau,

The semi-axes was not equal so we have an Ellipse. Than I decided to check if this point is the point of Ellipse and the Line Segment in the same time.

So we have 8 points (I like Symmetry sometimes ^^), that is points of the Ellipse and the Line Segment in the same time, during the motion of the Line Segment, I think it is enough to say that we have Ellipse trajectory of the all points, except three special :P .
And the further solution...

Well there is a thing with a crazy name - Eccentricity we can found those thing dividing the distance between focal stuff, by the largest self-axis of the Ellipse. For an example e of the Line will be 1, coz' as mr Maurice said, line is the extreme case of the Ellipse, where focal stuff is laying on the endpoints of the larger self-axis, the eccentricity of the Circle will be 0, coz' circle have only one focal stuff - this is means the distance between focuses is zero. The Ellipse have it's canonical equation, and in the process of obtain it in the book, I have found a formula for the eccentricity of the Ellipse (well I have not yet realized how the sum of the distances to the focal stuff in this bucket of formulas becoming definition of the large axis.. but it is a different story). b - smaller semi(half)-self-axis of the Ellipse, a - larger semi-self-axis (where the focal stuff placed) of the Ellipse. e - Eccentricity (for the Ellipse it must be between 0 and 1), L) - length of the segment.

So if we going to lay our segment on the Y-Axis, the coordinates of the our point tau will be actually larger semi-axis of the Ellipse that we think the trajectory of the point will be. Well we know that it will be somekind of the curved line, but which kind - to explore it, we need the Eccentricity that will define a type of the our curved trajectory.

If we going to lay our segment on the X-Axis, the coords. of tau point will be the length of the smaller semi-axis of our mentioned Ellipse, or the another curve :). Let's try to find the eccentricity by our two semi-axis.

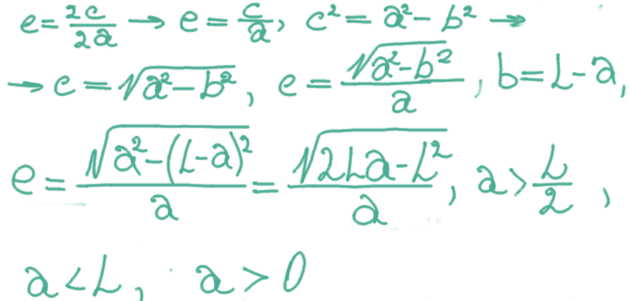
Well I have a mind activity like a Patrick the Star, to realize what I need to do next, but I have found this way - we can ZOOM in or ZOOM out, our Coordinates to obtain a coords = L, so we can express those crazy function like a something little bit smaller.

,

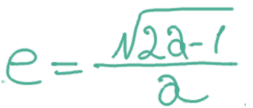So it is looks like our a semi-axis, to better not trun into zero, coz darn singularity will be :) , turning it to the something larger than 1, it is means than L (I hope so..), is looks weird too, the semiaxis of our extreme Ellipse - the line, is larger than actually line, it is restricted to the size of our segment - it means restricted to L, or in our units to 1. , when a = 1 (L), we will have e = 0, it means a circle. This is happens for the single point - for the center (I hope so).
We can subtract a form numerator of our e-function to look how it corresponds, larger or smaller.

I have done some calculation, I have tried to make a graph also (with low success, to hard for ma brain), it seems for two cases

1) a equals one-half, ---> one half is larger than zero, so numerator is positive, and the eccentricity is equal one.

2) a equals three-fourths, in these case three-fourths will be greater than square root from one-half,
well square root from one half divided by three-fourths will equal four square root from one-half, divide by three :hmm: And this will equal 2 square root of two divided by three, And that looks like less than 1 - ^^, nay, all looks +/- fine.

We have done all those stuff for the case when a is greater than zero, when a is greater than the half of L, and when a is less than 1, but due to the symmetry stuff, I hope it will be true for the other cases too. And of course we using coord. values only, no their signs, but I think if we going to say something about symmetry, this note will be unnecessary.
The problem, for myself is hard to understand why the center of the Ellipse-trajectories stuff is the same as the origin of our coords. that can be little bit aside from it, and how we can check it? Anyway... I am goin to sleep...
For now I am too sleepy to say something more, but I think it good enough for now...

THANX for the answers.

 

[Buffu]

@frostysh

What can be said about $\sin \theta$ and $\cos \theta$ based on the coordinates of $x$ and $y$ of P ?

If you know then just put those in $\sin^2 \theta + \cos^2 \theta = 1$.

 

[frostysh]

$$\sin{\theta} = \frac{y_{p}}{\left( PB \right)}, \cos{\theta} = \frac{x_{p}}{\left( AP \right)} \Rightarrow \frac{{y_{p}}^{2}}{{\left( PB \right)}^{2}} + \frac{{x_{p}}^{2}}{{\left( AP \right)}^{2}} = 1 \sim \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 \Rightarrow \text{An Ellipse!}$$ It is looks like a Ellipse stuff, our segments of our segment will be constant for the any particular P - point (well they will flip into each others, but due to the symmetry - it is ok), and if the point will be on center of our segment, the hypotenuses will be equal, so the denominators will be equal too, so it will be a Circle case. It's make a sense. And much more better than ma' attempt to solve.
Thanx.
Now I can move further - to hyperbolic thing, - I making some kind of self-education, and trying to get trough a book for a basic-college level Mathematical stuff. :P

P.S. I hate LATEX.

 

[Buffu]

$$\sin{\theta} = \frac{y_{p}}{\left( PB \right)}, \cos{\theta} = \frac{x_{p}}{\left( AP \right)} \Rightarrow \frac{{y_{p}}^{2}}{{\left( PB \right)}^{2}} + \frac{{x_{p}}^{2}}{{\left( AP \right)}^{2}} = 1 \sim \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 \Rightarrow \text{An Ellipse!}$$ It is looks like a Ellipse stuff, our segments of our segment will be constant for the any particular P - point (well they will flip into each others, but due to the symmetry - it is ok), and if the point will be on center of our segment, the hypotenuses will be equal, so the denominators will be equal too, so it will be a Circle case. It's make a sense. And much more better than ma' attempt to solve.
Thanx.
Now I can move further - to hyperbolic thing, - I making some kind of self-education, and trying to get trough a book for a basic-college level Mathematical stuff. :P

P.S. I hate LATEX.

You are welcome .

Which book you are using ? It might help me.

 

[frostysh]

Well, I have doubts about that, but if you want to know - "The Elements of the High Mathematics - for technicians" I. L. Zaycev, (Элементы Высшей Математики, для техникумов, И.Л. Зайцев), техникумы - on the crazy Russia language is means something like a high-school stuff, in the middle before University, and after the School level education.
Indeed, the Internet is the great thing, doesn't matter, who you are, where you from, you can try to find a help there - it is an amazing.