- #1
ecastro
- 254
- 8
1. The problem statement, aall variables, and given/known data
I need to find the angle between a point on the ellipse and the ellipse's center shown in the figure below:
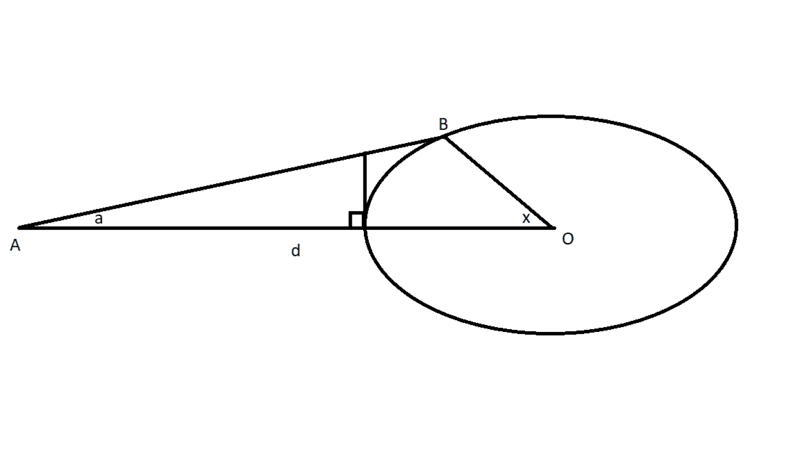
The known variables are 'd', the distance between point O (the center of the ellipse) and point A, and 'a', the angle, outside the ellipse, between the lines AO and AB. The ellipse has a major-axis of ##r_1## and a minor axis of ##r_2##. The needed angle is 'x', the angle between the lines AO and BO, inside the ellipse. Note, however, that the line AB is not tangent to the ellipse.
Edit: By the way, 'd' is equal to the sum of ##H## and ##r_1##.
Thank you in advance.
The relevant equations might be sines and cosines or even the sine and cosine laws. I am not sure since the line AB is not tangent to the ellipse.
I tried calculating the line perpendicular to AO to line AB (the opposite side of 'a' shown in the figure), but I do not know how to proceed then. The only solution I can think of is putting everything in a coordinate system and find the intersection of the line AB and the ellipse. Is there a more elegant solution than this one?
I need to find the angle between a point on the ellipse and the ellipse's center shown in the figure below:
The known variables are 'd', the distance between point O (the center of the ellipse) and point A, and 'a', the angle, outside the ellipse, between the lines AO and AB. The ellipse has a major-axis of ##r_1## and a minor axis of ##r_2##. The needed angle is 'x', the angle between the lines AO and BO, inside the ellipse. Note, however, that the line AB is not tangent to the ellipse.
Edit: By the way, 'd' is equal to the sum of ##H## and ##r_1##.
Thank you in advance.
Homework Equations
The relevant equations might be sines and cosines or even the sine and cosine laws. I am not sure since the line AB is not tangent to the ellipse.
The Attempt at a Solution
I tried calculating the line perpendicular to AO to line AB (the opposite side of 'a' shown in the figure), but I do not know how to proceed then. The only solution I can think of is putting everything in a coordinate system and find the intersection of the line AB and the ellipse. Is there a more elegant solution than this one?