Weird stuff on infinite numerical sequences in a Soviet book

[inthenickoftime]

TL;DR Summary

It looks like an undefined operation

The book is Calculus: Basic Concepts for High School
on the first page you are given the following sequence:

1, -1, 1/3, -1/3, 1/5, -1/5, 1/7, -1/7, ...

several pages later the rule is given:

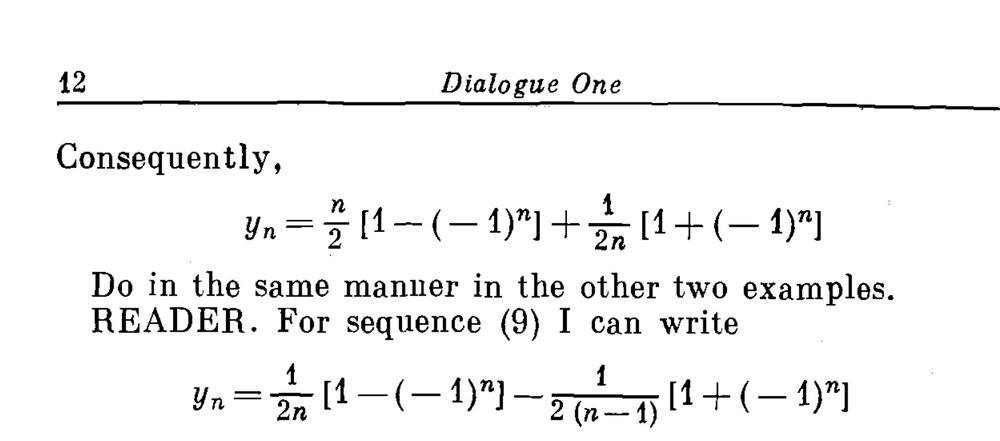
in the second rule, for the first term in the sequence, the coefficient of one of the terms is 1/0. How legitimate is this?

 

[member 587159]

Start with $n=2$ instead of $n=1$ or make a shift. For most purposes in analysis, leaving out finitely many terms of a sequence doesn't matter since we are mostly interested in the tail of the sequence.

 

[inthenickoftime]

Start with $n=2$ instead of $n=0$ or make a shift. For most purposes in analysis, leaving out finitely many terms of a sequence doesn't matter since we are mostly interested in the tail of the sequence.

It still feels weird. On the previous page the author gives his definition of an infinite numerical sequence as a rule assigning every natural number to a definite term in the sequence, but 1 doesn't correspond with anything, at least for the given expression. But I see what you mean

 

[PeroK]

It still feels weird. On the previous page the author gives his definition of an infinite numerical sequence as a rule assigning every natural number to a definite term in the sequence, but 1 doesn't correspond with anything, at least for the given expression. But I see what you mean

You can define a sequence on any infinite subset of the natural numbers. In other words, you can do things like:

Define the sequence for $n = n_0, n_0 +1, n_0 + 2 \dots$, where $n_0$ can be any starting number.

Define the sequence for odd, even or square or prime $n$. For example, you could define a sequence as $a_n$, where $n$ is prime.

That said, in all these cases you ought to make clear the restriction on $n$. E.g. $n \ge 2$ or $n$ even or $n$ prime etc.

 

[inthenickoftime]

You can define a sequence on any infinite subset of the natural numbers. In other words, you can do things like:

Define the sequence for $n = n_0, n_0 +1, n_0 + 2 \dots$, where $n_0$ can be any starting number.

Define the sequence for odd, even or square or prime $n$. For example, you could define a sequence as $a_n$, where $n$ is prime.

That said, in all these cases you ought to make clear the restriction on $n$. E.g. $n \ge 2$ or $n$ even or $n$ prime etc.

No restrictions were given. You can check the book online for free, it was rewritten in modern style. Too bad as I was really looking forward to it.

 

[mfb]

The y_n pattern listed there only applies to n>1, for y₁ it does not apply. If you care about the absolute value of the limit you need to consider y₁ separately, if you only care about convergence you do not.