- #1
Calculuser
- 49
- 3
There is a statement on page 26 in Elliott Mendelson's book of "Introduction to Mathematical Logic" as shown:
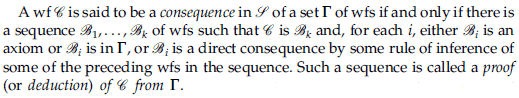
What I got from the statement above, which is obvious, I guess, is that in the sequence of [itex]\mathcal{B}_1,\mathcal{B}_2,...\mathcal{B}_k[/itex] there are "SOME" well-formed formulas (wfs) that elements of [itex]\Gamma[/itex] set of wfs, or axioms that are NOT elements of [itex]\Gamma[/itex], or direct consequences by some rule of inference of some the preceding wfs in the sequence. To me, It also seem to be possible that "ALL" of those [itex]\mathcal{B}_k[/itex] wfs can by definition be one of the three possibilities mentioned above. Hence, we cannot say [itex]\Gamma=\{\mathcal{B}_1,\mathcal{B}_2,...\mathcal{B}_k\}[/itex].
My questions in regard to these are:
1) Does [itex]\mathcal{L}(\mathcal{B}_k=\mathcal{L})[/itex] has to be in the set of [itex]\Gamma[/itex] or not?
2) What exactly does [itex]\Gamma[/itex] represent?
What I got from the statement above, which is obvious, I guess, is that in the sequence of [itex]\mathcal{B}_1,\mathcal{B}_2,...\mathcal{B}_k[/itex] there are "SOME" well-formed formulas (wfs) that elements of [itex]\Gamma[/itex] set of wfs, or axioms that are NOT elements of [itex]\Gamma[/itex], or direct consequences by some rule of inference of some the preceding wfs in the sequence. To me, It also seem to be possible that "ALL" of those [itex]\mathcal{B}_k[/itex] wfs can by definition be one of the three possibilities mentioned above. Hence, we cannot say [itex]\Gamma=\{\mathcal{B}_1,\mathcal{B}_2,...\mathcal{B}_k\}[/itex].
My questions in regard to these are:
1) Does [itex]\mathcal{L}(\mathcal{B}_k=\mathcal{L})[/itex] has to be in the set of [itex]\Gamma[/itex] or not?
2) What exactly does [itex]\Gamma[/itex] represent?