sroeyz
- 5
- 0
Hello, I wish to show that on 3-dimensional manifolds, the weyl tensor vanishes.
In other words, I want to show that the curvature tensor, the ricci tensor and curvature scalar hold the relation
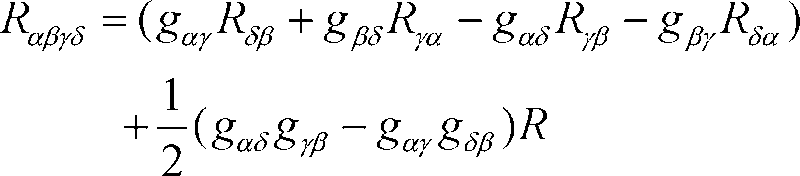
Please, if anyone knows how I can prove this relation or refer to a place which proves the relation, I will be most grateful.
Thanks in advance
In other words, I want to show that the curvature tensor, the ricci tensor and curvature scalar hold the relation
Please, if anyone knows how I can prove this relation or refer to a place which proves the relation, I will be most grateful.
Thanks in advance