JD_PM
- 1,125
- 156
- Homework Statement
- 1) Get the coordinates of both the lower and upper cylinders.
2) Combine the two given equations to get the given result.
- Relevant Equations
- 1) ##( x_1 + 2R \sin \theta, 3R - 2(R-\cos \theta))##
2) Combine
$$\frac 1 2 M R^2 \Big( 3 \dot \theta_1^2 + 2 \dot \theta_1 \dot \theta(1 - 2 \cos \theta) + 6 \dot \theta^2 \Big) + 2MR(1 + \cos \theta)g = 4MRg \ \ \ \ (1)$$
$$MR^2 \Big(3 \dot \theta_1 + \dot \theta ( 1 - 2 \cos \theta) \Big)=0 \ \ \ \ (2)$$
To get
$$\dot \theta^2 \Big( 18 - (1 - 2 \cos \theta)^2 \Big) = \frac 12 R (1 -\cos \theta) g$$
I was solving a problem and got stuck in two aspects:
1) Geometric issue.
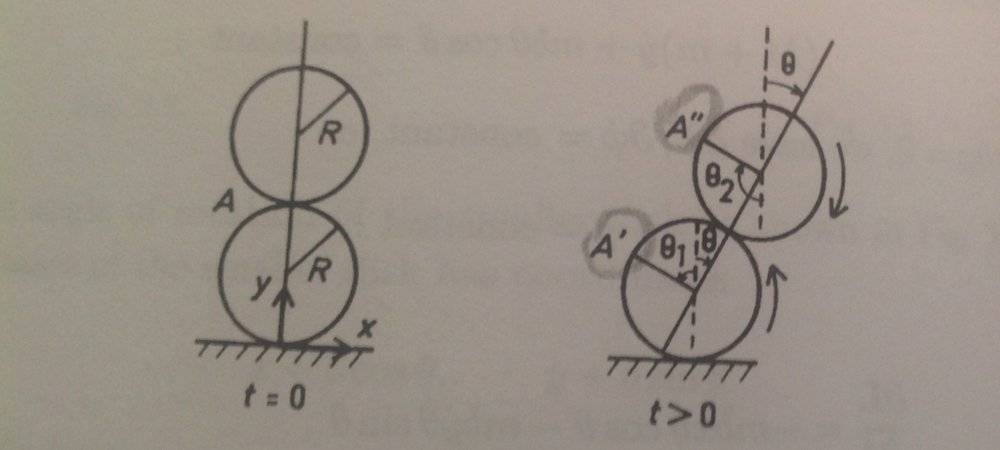
Alright, I understand that the coordinates of the lower cylinder are
$$( -R \theta_1, R)$$
The coordinates of the upper cylinder are:
$$( x_1 + 2R \sin \theta, 3R - 2(R-\cos \theta))$$
I get that the ##x## coordinate of the upper cylinder is ##x_2 = x_1 + 2R \sin \theta##
But I do not understand why ##y_2 = 3R - 2(R-\cos \theta)##.
2) Algebraic issue
I have the following two equations:
$$\frac 1 2 M R^2 \Big( 3 \dot \theta_1^2 + 2 \dot \theta_1 \dot \theta(1 - 2 \cos \theta) + 6 \dot \theta^2 \Big) + 2MR(1 + \cos \theta)g = 4MRg \ \ \ \ (1)$$
$$MR^2 \Big(3 \dot \theta_1 + \dot \theta ( 1 - 2 \cos \theta) \Big)=0 \ \ \ \ (2)$$
There has to be a way to combine them such that we eliminate ##\theta_1## to get:
$$\dot \theta^2 \Big( 18 - (1 - 2 \cos \theta)^2 \Big) = \frac 12 R (1 -\cos \theta) g$$
But I do not see it. What I have done is multiply the second equation by ##-\frac{\dot \theta_1}{2}## and then add both up. Like that I just get rid of the first terms of both equations.
Could you please give me some hints on 1) and 2) issues?
Thanks.
1) Geometric issue.
Alright, I understand that the coordinates of the lower cylinder are
$$( -R \theta_1, R)$$
The coordinates of the upper cylinder are:
$$( x_1 + 2R \sin \theta, 3R - 2(R-\cos \theta))$$
I get that the ##x## coordinate of the upper cylinder is ##x_2 = x_1 + 2R \sin \theta##
But I do not understand why ##y_2 = 3R - 2(R-\cos \theta)##.
2) Algebraic issue
I have the following two equations:
$$\frac 1 2 M R^2 \Big( 3 \dot \theta_1^2 + 2 \dot \theta_1 \dot \theta(1 - 2 \cos \theta) + 6 \dot \theta^2 \Big) + 2MR(1 + \cos \theta)g = 4MRg \ \ \ \ (1)$$
$$MR^2 \Big(3 \dot \theta_1 + \dot \theta ( 1 - 2 \cos \theta) \Big)=0 \ \ \ \ (2)$$
There has to be a way to combine them such that we eliminate ##\theta_1## to get:
$$\dot \theta^2 \Big( 18 - (1 - 2 \cos \theta)^2 \Big) = \frac 12 R (1 -\cos \theta) g$$
But I do not see it. What I have done is multiply the second equation by ##-\frac{\dot \theta_1}{2}## and then add both up. Like that I just get rid of the first terms of both equations.
Could you please give me some hints on 1) and 2) issues?
Thanks.
