Darkmisc
- 222
- 31
- Homework Statement
- The domain of cos is restricted to [0, pi]. What is the implied domain and range of cos(tan^-1(x))?
- Relevant Equations
- y=cos(tan^-1(x))?
Hi everyone
I have the solution to this question, but I'm not sure I understand it.


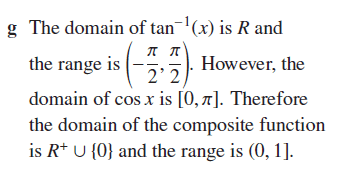
Why is the domain of the composite function
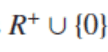 and not [0, pi]?
and not [0, pi]?
Is it because tan^-1 (0 and R+) will always give a value between (-pi/2, pi/2)? I.e. the domain of the composite function refers to x.
Is 0 excluded from the range of the composite function because pi/2 is excluded from the domain of tan^-1?
Thanks
I have the solution to this question, but I'm not sure I understand it.
Why is the domain of the composite function
Is it because tan^-1 (0 and R+) will always give a value between (-pi/2, pi/2)? I.e. the domain of the composite function refers to x.
Is 0 excluded from the range of the composite function because pi/2 is excluded from the domain of tan^-1?
Thanks