stunner5000pt
- 1,447
- 5
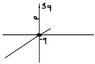
Two point charges 3q and iq are spearated by distance a as in the diagram. Find the monopole, dipole moments and the approximate potential at large (in spherical coords including both dipole and monopole contributions)
monopole moment is sum of charges 3q \hat{k} + qa \hat{k} = q(a+2) \hat{k}
dipole moment is (assume that the origin is located half way between the two cahrges
then
p= 3q \frac{a}{2} \hat{k} + (-q}\frac{a}{2} \hat{k} = 2qa \hat{k}
also
\overline{p} = p + qa\hat{k}
\overline{p} = qa \hat{k}
is this correct?
where di i got wrong? with the transofmration of coordinates? With the way i calculated p?? When i calculate the potential the dipole moment will point radially in the z direction hence \hat{k} = \hat{r} \cos\theta [/tex]<br /> <br /> thank you for your help and responses!
monopole moment is sum of charges 3q \hat{k} + qa \hat{k} = q(a+2) \hat{k}
dipole moment is (assume that the origin is located half way between the two cahrges
then
p= 3q \frac{a}{2} \hat{k} + (-q}\frac{a}{2} \hat{k} = 2qa \hat{k}
also
\overline{p} = p + qa\hat{k}
\overline{p} = qa \hat{k}
is this correct?
where di i got wrong? with the transofmration of coordinates? With the way i calculated p?? When i calculate the potential the dipole moment will point radially in the z direction hence \hat{k} = \hat{r} \cos\theta [/tex]<br /> <br /> thank you for your help and responses!
Last edited: