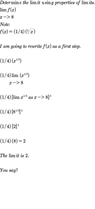What Are the Properties of Limits in Mathematics?
- Thread starter nycmathguy
- Start date
-
- Tags
- Limits Properties
Click For Summary
The discussion centers on the properties of limits in mathematics, specifically focusing on the limit of a function as it approaches a point of interest. The limit of the function f(x) as x approaches 8 is definitively established as 1/2, regardless of the value assigned to f(8). The conversation emphasizes that limits consider the behavior of a function around a point rather than the value at that point, highlighting the concept of continuity and discontinuity. The participants suggest that understanding these concepts is essential and should be covered in calculus textbooks.
PREREQUISITES- Understanding of limits in calculus
- Familiarity with continuity and discontinuity concepts
- Basic knowledge of functions and their behaviors
- Experience with mathematical notation and expressions
- Study the definition and properties of limits in calculus
- Explore continuity and discontinuity in functions
- Learn about the epsilon-delta definition of limits
- Review examples of limits involving piecewise functions
Students studying calculus, educators teaching mathematics, and anyone interested in understanding the foundational concepts of limits and their implications in mathematical analysis.
Similar threads
- · Replies 4 ·
- · Replies 22 ·
- · Replies 5 ·
- · Replies 12 ·
- · Replies 9 ·
- · Replies 1 ·
- · Replies 20 ·
- · Replies 5 ·
- · Replies 3 ·
- · Replies 7 ·