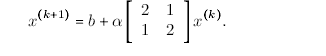SUMMARY
The discussion focuses on determining the values of α for which the iteration converges in a linear system defined by the equation x(n+1) = b + αAx(n). It is established that the condition for convergence is ||αA|| < 1, where ||·|| denotes the matrix norm. Specifically, this implies that |α| must be less than 1/||A||, ensuring that the worst-case error in the initial value x(0) is minimized. The matrix A is defined as a 2x2 matrix with elements [[2, 1], [1, 2]].
PREREQUISITES
- Understanding of linear systems and iteration methods.
- Familiarity with matrix norms and their properties.
- Knowledge of first-order difference equations.
- Basic concepts of numerical stability in iterative methods.
NEXT STEPS
- Study matrix norms in detail, particularly in the context of convergence analysis.
- Learn about the implications of the spectral radius on iterative methods.
- Explore the stability criteria for linear systems and their applications.
- Investigate the role of difference equations in numerical analysis.
USEFUL FOR
Mathematicians, engineers, and computer scientists involved in numerical analysis, particularly those working with iterative methods and linear systems.