What are these two: ##L_{i}## & ##L_{f}##?

[Benjamin_harsh]

Homework Statement

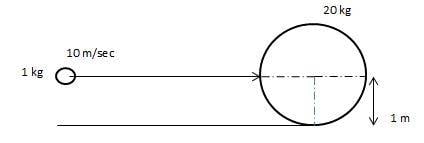
A 1 kg mass of clay, moving with a velocity of 10 m/s, strickes a stationary wheel and sticks to it. The solid wheel has a mass of 20 kg and a radius of 1m. Assuming that the wheel is set into pure rolling motion, the angular velocity of the wheel immediately after the impact is approximately.

Relevant Equations

$L_{i} = mvr = 1*10*1 = 10$,
$L_{f} = mv_{cm}r + Iω$

A 1 kg mass of clay, moving with a velocity of 10 m/s, strickes a stationary wheel and sticks to it. The solid wheel has a mass of 20 kg and a radius of 1m. Assuming that the wheel is set into pure rolling motion, the angular velocity of the wheel immediately after the impact is approximately.

Sol:

$L_{i} = mvr = 1*10*1 = 10$
$L_{f} = mv_{cm}r + Iω$
$= 20*rω*r + (mr^2 ω)/2 = 20ω + 10ω$
$L_{f} =30 ω$
$L_{i} = Lf$
$10 = 30 ω$
$ω = \large\frac {1}{3} \;\normalsize rad/sec$

What are these two: $L_{i}$ & $L_{f}$?

 

[Orodruin]

Initial and final angular momentum?

 

[Baddum12]

Generally, subscripts "i" and "f" refer to "initial" and "final" values of a particular quantity. In addition, the capital "L" usually refers to angular momentum.

Combine these pieces of information and you should have a good idea on what these variables refer to. In fact, you can use the given equations for L to confirm that it is indeed angular momentum.

 

[Benjamin_harsh]

final angular momentum?

Why we have to add $Iω$ to final angular momentum; $L_{f}$?

What does $v_{cm}$ mean?

 

[Orodruin]

Why we have to add $Iω$ to final angular momentum; $L_{f}$?

The angular momenta are with respect to the contact point of the wheel with the ground (if it would not be, angular momentum would not be conserved because there are forces acting there such as friction). Knowing that, it is just an application of the parallel axis theorem.

What does $v_{cm}$ mean?

It is kind of standard notation for the center of mass velocity.

Edit: Note that the solution is wrong. It is not taking into account that the mass of the clay after impact. As the mass is 1/20 of the wheel's mass, the error introduced by this should be expected to be in the range 2-15% or so.

 

[Benjamin_harsh]

Assuming that the wheel is set into pure rolling motion does it mean clay used to roll the wheel here or wheel is already in rolling motion before clay strikes it?

 

[Orodruin]

The problem formulation states that the wheel is stationary before being hit by the clay.

 

[Benjamin_harsh]

In this two steps: $L_{f} = mv_{cm}r + Iω$

$= 20*rω*r + \large \frac{mr^2 ω}{2}\normalsize = 20ω + 10ω$

How $I = \large\frac{mr^{2}}{2}$ ?

 

[Orodruin]

That is one of the standard results for moments of inertia. In this case the moment of inertia of a solid disk relative to its center. If you do not know how to compute or look up moments of inertia, you should probably study this in a textbook.

 

[Benjamin_harsh]

Is center of mass velocity; $V_{cm}$ of any circle is $rω$ ?

 

[Orodruin]

For a rolling circle, yes.

To be perfectly honest, it seems to me that you do not control the basics needed to attempt this problem and understand it. In all well-meaning, I would suggest that you go back to the basics regarding rolling motion, kinematics, and conservation of angular and linear momentum before going further here.

 

[Benjamin_harsh]

Why we have to consider center of mass velocity of a rolling circle to calculate its angular momentum?

 

[Orodruin]

See previous answer. I suggest that you go back to remind yourself about the basics of angular momentum before attempting to understand this problem further.

 

[Benjamin_harsh]

Just to be clear, it's rotating in the Z-axis (into the page), but moving (due to rolling) in the x-axis. I am confused..

 

[haruspex]

Why we have to consider center of mass velocity of a rolling circle to calculate its angular momentum?

It is very important to understand that torque, moment of inertia and angular momentum are each relative to an axis. For the angular momentum about the mass centre the linear velocity doesn’t matter, but here the solver has chosen an axis at ground level.
If a particle mass m at position $\vec r$ relative to the axis is moving with velocity $\vec v$ then its angular momentum about the axis is $m\vec r\times\vec v$. In the question above, the clay starts with angular momentum mvr about an axis on the ground.
There is a good reason for choosing the axis at ground level. When the clay hits the wheel we are told that the wheel immediately commences rolling motion. That implies there is a strong frictional force at the ground to prevent slipping. (A toothed wheel on a toothed rack would be a good model.) By choosing the axis at ground level, this force exerts no torque, so angular momentum about it is conserved.