What Determines the Axes of an Elliptical Orbit?

[Karol]

Homework Statement

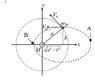
A satellite of mass m rotates in a circle of radius a round a star of mass M.
At point P it's velocity V₀ is altered to be parallel to the x axis.
The trajectory becomes an ellipse. show that the axes of the ellipse are a and b.

Homework Equations

Potential energy:
U=-\frac{gMn}{R}
Total energy of a satellite: E_tot=U+E_k
The ellipse definition: the trajectory of a rope of fixed length, attached on both it's ends.

The Attempt at a Solution

The solution is that the kinetic energy increases monotonically from point A to point B, and so there is only one point, which is P, at which: E_tot=-E_k=|U/2|.
And, from geometry, the distance from the ellipse focus to P equals a, which i understand, so, the ellipse's axes must be a and b.
What i don't understand is why the condition E_tot=-E_k=|U/2| must occur specifically at point P.
I understand that U changes linearly with the distance R, and that U is symmetric around point P: at point A it is less the same amount that it is higher at point B, but still i think that the condition E_tot=-E_k=|U/2| may occur at other points on the ellipse

 

[gneill]

Since the orbit change occurs from an initially circular orbit, the radius must be of length a. The velocity is also specified to be Vo for both the circle and the ellipse. So you can write the expression for the total energy (specific energy $\xi$).

You should also know an expression for the specific energy of an orbit in terms of its major axis and the gravitational parameter μ. Equate, isolate KE.

 

[Karol]

I don't know what specific energy is, i know what potential and kinetic energies are, and that their sum is the total energy of the satellite.
Where can i read about specific energy?

 

[mfb]

Total energy in the Kepler problem depends on the semi-major axis only (and the masses and G of course) - the energy is not modified, so the semi-major axis of the ellipse is "a" as well.
Specific energy is just the total energy divided by the mass of the satellite - as it does not change its mass, it does not matter which one you use.

 

[gneill]

I don't know what specific energy is, i know what potential and kinetic energies are, and that their sum is the total energy of the satellite.
Where can i read about specific energy?

Specific energy is just the energy terms without the mass. Thus, for example, the specific kinetic energy is V²/2. Think of it as being the energy per unit mass for the object in question. The total specific energy for an orbit is

$$\xi = \frac{V^2}{2} - \frac{\mu}{r}$$

 

[Karol]

Total energy in the Kepler problem depends on the semi-major axis only (and the masses and G of course) - the energy is not modified, so the semi-major axis of the ellipse is "a" as well.

I know only that the total energy is E_tot=-GMm/2a because i started and derived this equation from a circular trajectory, i know nothing about total energy in the kepler problem.
Can this equation be derived for an elliptic orbit of it's own, without connection to a circular movement? then i will understand it relates to the semi-major axis of an ellipse.
And, what is a semi-major axis of an ellipse? isn't it a in my drawing?
And how is b called?

Edit by Borek: please attach only png/gif/jpg images, not bmp.

 

[gneill]

A circular orbit is a "special case" of an elliptical orbit where the eccentricity happens to be zero

Your equation for E_tot includes the mass of the satellite, m. If you drop the m you have the specific mechanical energy for the orbit: $\xi = -\frac{G M}{2 a}$. Now, when M >> m then $\mu ≈ GM$. So that $\xi = -\frac{\mu}{2a}$.

This relates the specific mechanical energy of the orbit to the size of the semi-major axis of the orbit, a, which is half the length of the long axis of the ellipse as in your drawing. The perpendicular axis (across the "width" of the ellipse) is known as the minor axis. Half of it is b, the semi-minor axis.

So now you have two equations for the specific mechanical energy. Equate them and plug use the given information for the point P.

 

[mfb]

Can this equation be derived for an elliptic orbit of it's own, without connection to a circular movement?

It can.

And, what is a semi-major axis of an ellipse? isn't it a in my drawing?

Half the major axis (the longer axis in the ellipse), and identical to the distance between focal points and the points at the ends of the minor axis (P in your sketch). This geometric identity can be used to show that P is really on the minor axis of the ellipse.

 

[Karol]

How can the equation E_tot=-GMm/2a be derived for an ellipse, without connection to a circle, and how can it be shown that a is the semi-major axis?

 

[gneill]

How can the equation E_tot=-GMm/2a be derived for an ellipse, without connection to a circle, and how can it be shown that a is the semi-major axis?

It involves a consideration of the constants of the motion that come from the trajectory equation for a body in orbit (the differential equation describing the motion). For a derivation, I refer you to a text on orbital mechanics. In particular, I recommend Fundamentals of Astrodynamics by Bate, Mueller, and White. It's a rather inexpensive softcover that covers the topic quite well.

 

[Karol]

I didn't receive an answer to my initial question.
Why, when the velocity's direction changes, the ellipse is in the shape, size and position as in my drawing?
Why is it's major axis a, the same as the circle's radius?
I was told that since the kinetic energy grows, monotonically, from A to B, there is one point at which Etot=-Ek=|U/2|, and this is P.
Why, necessarily, P? it could occur on other points on the ellipse.

 

[gneill]

I didn't receive an answer to my initial question.
Why, when the velocity's direction changes, the ellipse is in the shape, size and position as in my drawing?
Why is it's major axis a, the same as the circle's radius?
I was told that since the kinetic energy grows, monotonically, from A to B, there is one point at which Etot=-Ek=|U/2|, and this is P.
Why, necessarily, P? it could occur on other points on the ellipse.

The problem states that the change makes the velocity parallel to the x-axis at point P. The Sun is the focus which lies on the x-axis. By symmetry then, the point P must lie at an end of the minor axis -- nowhere else on the ellipse is the trajectory parallel to the major axis.

When you construct an ellipse using two pins and a thread, the pins being stuck into the two foci, the thread with length 2a tied to the pins, and a pencil run around the perimeter bounded by the taut thread, then the sum of the two radii defined by the pencil-to-pin thread sections is a constant 2a.

In the figure, r + r' = 2a. Now, when the pencil reaches the vertical mid line of the ellipse, r = r' so then r = a.

 

[Karol]

The situation could have been like this, with a the radius of the circle.
In this case the velocity is parallel to the initial x-axis also, and a isn't the major axis.

 

[gneill]

The situation could have been like this, with a the radius of the circle.
In this case the velocity is parallel to the initial x-axis also, and a isn't the major axis.

No, the original diagram for the problem indicates that the major axis of the intended ellipse lies along the x-axis.

Also, not just any ellipse will do -- it must have a total energy consistent with the kinetic and potential energy at the instant it is created (at the course change). A body on a circular orbit of radius a has an orbital velocity of $v_o = \sqrt{\mu/a}$. So its specific kinetic energy, being $v_o^2/2$, is $\mu/(2a)$. The specific PE is $-\mu/a$. That means the total specific energy is
$$\xi = \frac{\mu}{2a} - \frac{\mu}{a}$$
This simplifies to
$$\xi = -\frac{1}{2}\frac{\mu}{a}$$
in other words, (minus) half the PE.

 

[Karol]

leave out the initial drawing, it tries to prove that the situation is in that manner.
Maybe it is, it could be different.
The ellipse doesn't necessarily create itself according to the drawings.

 

[gneill]

No matter what set of axes you choose, the initial kinetic and potential energies are fixed by the conditions of the problem; distance is the radius of the circular orbit, a, and speed is that of the circular orbit speed, $\sqrt{\mu/a}$. This fixes the energy of the orbit:

$\xi = \frac{\mu}{2a} - \frac{\mu}{a} = -\frac{\mu}{2a}$

Now, for all orbits the specific mechanical energy is related to the semi-major axis a by:

$\xi = -\frac{\mu}{2a}$

By inspection we conclude that the a's are the same in both cases, namely semi-major axis of the ellipse.