What Does the Wave Function Reveal About k and ω?

[evinda]

Hello! (Wave)

A function of the form

$$u(x,t)=A \cos{(kx-\omega t)}, \text{ where } k>0, \omega>0, A>0$$

is called wave function. If in addition $u(x,t)$ is the solution of a differential equation with partial derivatives we are talking about a solution of the differential equation in the form of a wave function.
$k$ is called wavenumber and $\omega$ is called circular frequency.

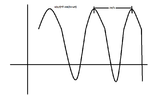
$k$ counts the cycles that the wavefunction makes at the space interval of length $2 \pi$-in respect to $x$.View attachment 4140What does $\frac{2 \pi}{k}$ represent? What does it count?

 

[I like Serena]

What does $\frac{2 \pi}{k}$ represent? What does it count?

Hey! (Wink)

$\frac{2 \pi}{k}$ is the wave length, usually represented by the symbol $\lambda$. (Wasntme)

It is similar to the period $T$ of a wave, for which we have $\omega = \frac{2\pi}{T}$.
You may also run into the frequency $f$ of the wave, which is $f = \frac{1}{T}$.

The velocity $v$ (or sometimes $c$) of a wave is its wave length $\lambda$ divided by its period $T$. (Nerd)

 

[evinda]

Hey! (Wink)

$\frac{2 \pi}{k}$ is the wave length, usually represented by the symbol $\lambda$. (Wasntme)

It is similar to the period $T$ of a wave, for which we have $\omega = \frac{2\pi}{T}$.
You may also run into the frequency $f$ of the wave, which is $f = \frac{1}{T}$.

The velocity $v$ (or sometimes $c$) of a wave is its wave length $\lambda$ divided by its period $T$. (Nerd)

Then there is the following definition:

$\omega$ counts the cycles that the wave function makes in the time interval $2 \pi$- in respect to $t$.

So $\frac{2 \pi}{\omega}$ is equal to the period, right?
Can we see it at the above graph? Or would we have to draw an other one? (Thinking)

 

[I like Serena]

Then there is the following definition:

$\omega$ counts the cycles that the wave function makes in the time interval $2 \pi$- in respect to $t$.

So $\frac{2 \pi}{\omega}$ is equal to the period, right?
Can we see it at the above graph? Or would we have to draw an other one? (Thinking)

Yep. That's the period.

And we would need another graph. (Wasntme)

The graph you have is of $u(x,t)$ versus $x$, where $t$ has some fixed value.
You're talking about a graph of $u(x,t)$ versus $t$, with a fixed $x$ value. (Thinking)

 

[evinda]

Yep. That's the period.

And we would need another graph. (Wasntme)

The graph you have is of $u(x,t)$ versus $x$, where $t$ has some fixed value.
You're talking about a graph of $u(x,t)$ versus $t$, with a fixed $x$ value. (Thinking)

Ah, I see... So it will be exactly the same graph with the only difference that the perpendicular axis will represent $t$ instead of $x$. Right? (Thinking)

 

[I like Serena]

Ah, I see... So it will be exactly the same graph with the only difference that the perpendicular axis will represent $t$ instead of $x$. Right? (Thinking)

Yep. (Nod)

 

[evinda]

Yep. (Nod)

Great! Thanks a lot! (Angel)