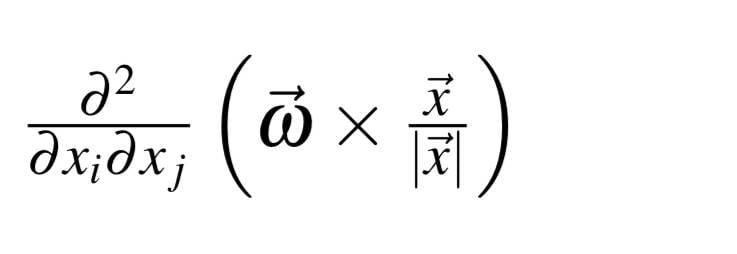No. Because the function is symmetric in the three parameters, you can replace them with ##x_i##, ##x_j##, ##x_k##, where it is understood that {i,j,k}={1,2,3}, but which is which is unspecified.
For example, suppose you had the function ##x_1x_2x_3## then its partial derivative wrt ##x_i## and ##x_j## would be ##x_k##.
Edit, you might also need to assume that i, j, k are in the same cyclic order as 1, 2, 3.
Edit 2: Just realised my posts may be off the mark. I need to solve it myself first.
Edit 3:
Rereading the question, I see it does not refer to indices 1, 2, 3. That is something you assumed. So my correct answer to your post #3 is:
Yes, they are using i, j, k as the indices, not 1, 2, 3.