What does this notation mean? (suffix/prefix on tensors?)

[sa1988]

Looking at relativistic transformations and suddenly we have this transformation matrix with an upper and lower index. See below:

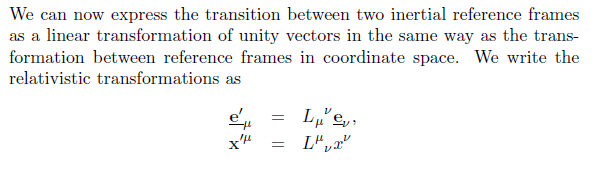
A bit of googling tells me the upper index means a co-ordinate. However I'm not sure what the lower index is. Overall I have no idea what makes it so special, or how to perform the operation in any way different from the sort of index notation I've already come across in fluid dynamics, wherein we have things like this for the divergence of a tensor:

$$\nabla \cdot A = \frac{\partial}{\partial x_i}A_{ij} $$

I simply don't get what's going on with the sudden separation into upper and lower indices here. Any advice would be appreciated, thanks.

 

[FactChecker]

In tensor analysis, there are covariant and contravariant indices. The lower and upper indices are used to distinguish between the two. Lower indices are covariant and upper indices are contravariant. With a contravariant index, when a unit of measure is converted to a smaller one, the associated number of units gets larger (e.g. conversion of 1 hour to 3600 seconds). With a covariant index, when a unit of measure is converted to a smaller one , the associated number gets smaller ( e.g. 1 mile/hour conversion to 1/3600 miles/sec ). You can find a more formal explanation, which still attempts to keep some intuitive motivation, in http://www.ita.uni-heidelberg.de/~dullemond/lectures/tensor/tensor.pdf

When you are dealing with a mixture of "units" and "per unit", it is helpful to have a methodical way of keeping things organized.

 

[sa1988]

In tensor analysis, there are covariant and contravariant indices. The lower and upper indices are used to distinguish between the two. Lower indices are covariant and upper indices are contravariant. With a contravariant index, when a unit of measure is converted to a smaller one, the associated number of units gets larger (e.g. conversion of 1 hour to 3600 seconds). With a covariant index, when a unit of measure is converted to a smaller one , the associated number gets smaller ( e.g. 1 mile/hour conversion to 1/3600 miles/sec ). You can find a more formal explanation, which still attempts to keep some intuitive motivation, in http://www.ita.uni-heidelberg.de/~dullemond/lectures/tensor/tensor.pdf

When you are dealing with a mixture of "units" and "per unit", it is helpful to have a methodical way of keeping things organized.

Great stuff, thanks for that. Extremely helpful little document!

EDIT: So just to make sure I'm on the right track: Raised indices are contravariant vectors, i.e. if you change the basis, the vectors change 'contrary' to that because they essentially have to be changed in the opposite direction of the basis change. Covariant vectors are ones that change with the basis.

The place I bumped into this confusion was in the relativistic kinematics section of the advanced mechanics module I'm doing. I hope I'd be right in thinking that the raised index in this context is spatial co-ordinates as they will surely be contravariant with respect to lorentz transforms which essentially alter the bases from which the situation is being looked at, whereas the lower index is time, which sticks to the time axis on, for example, a Minkowski diagram.

So, in a space-time vector (ct, x1, x2, x3) , we have (covariant, contravariant, contravariant, contravariant)

Is this right?