What exactly does the second derivative represent

[mycotheology]

I'm a visual thinker so I struggle a bit to get my head around calculus concepts. So as an example, here's a potential energy surface:

lets say this represents the structure of a simple molecule like n-propane:

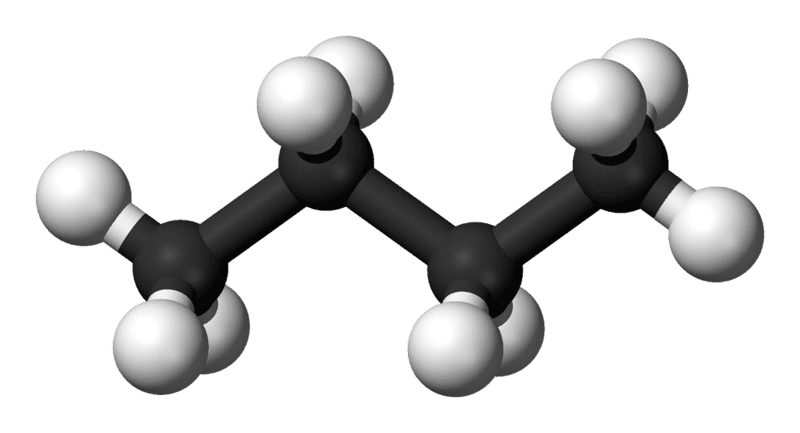
the molecule in the picture is the most stable conformation so the global minimum (the big pit) on the PES represents that conformation. Then the local minimum (the little bit) represents the staggered conformation. If I rotate or stretch the bonds in any other way, then it becomes less stable so the molecules energy will no longer be represented by a minimum on the PES.

I can see how the first derivative will help you locate the minima because the slope will be 0 there. The first derivative of this potential energy surface is called the "force" which makes sense to me because the y-axis represents the potential energy so when the molecule is in a stable conformation, the force which would ordinarily push the molecule into a stable conformation (if it was in an unstable one) is 0. What I'm trying to get my head around now is what the 2nd derivative represents. They call it the "force constant" and I know that in computational chemistry, they'll calculate the "force constant matrix" for a molecule. I'm trying to figure out what that means.

 

[chiro]

Hey mycotheology.

Mathematically, the 2nd derivative tells you how quickly one particular first derivative is changing. So if for example if the second derivative is negative it means, the first derivative is decreasing and if it's positive, then it means the first derivative is increasing.

In terms of turning points, if you have a minimum, then you expect the appropriate second derivative to be increasing since turning around means that things are "slowing down" and then turning around means that the derivative will keep increasing.

Now in terms of your matrix that you are talking about, I think this is going to refer to what is called the Hessian:

http://en.wikipedia.org/wiki/Hessian_matrix

Now if you are evaluating a second derivative at a particular turning point, this will tell you how rapidly this first derivative is increasing (if it's a minimum). I don't know about the physical or chemical applications so I won't comment on that.

If you can relate what the interpretation of the rate of change of the first rate of change corresponds to physically (so you say the first derivative corresponds to force which means in a physical analogy, the second derivative would correspond to "jerk" but I don't know if that's really valid), then you can look at the Hessian and see what this one attribute corresponds to with regard to what is contained in the derivative expressions.