What forces should be included?

[Doppler]

Hi,
I think that this question need the idea of torque.
But i m get stuck in choosing which point and what forces should be included.
Here it is :

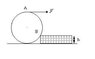
A cylinder with mass m=50kg located as shown in the figure.
Given that h = 0.5r
A force F is applied tangentially to the axle to lift the cylinder.
The minimum value of F is ________

 

[gnpatterson]

Hint: as the cylinder moves over the step there is a point that will have complicated normal and frictional forces. That is the point that you most want to leave out of your analysis so that is the point that you to calculate the moments about.

 

[FredGarvin]

Remember your basic statics equation, \Sigma M = 0.

The toughest part will be to figure out the relation of the contact point B to the center of the cylinder. You will have two forces at work, the weight of the cylinder and the force, F. They will both be acting about B.

Get your free body diagram going and see what you can reason out from there. You're on the right track with thinging about torque (moments).

 

[Doppler]

How about the normal force acting on the cylinder?
Why it is not in consideration?

 

[Doc Al]

Reread gnpatterson's hint. What point will you choose as the pivot for computing torques? Will the normal force exert a torque about that point?

 

[Doppler]

I mean,the normal force act on the cylinder by the floor.

 

[Doc Al]

When the cylinder loses contact with the floor, that normal force becomes zero.

 

[Doppler]

Thanks :D

I got my answer F=283N

Is that right?

 

[Doc Al]

Looks right to me.