- #1
lorenz0
- 148
- 28
- Homework Statement
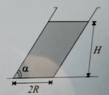
- A slanted cylinder of negligible mass has radius ##R=0.3m## and an internal angle of ##\alpha=70°## lies on a flat surface and is filled up with a liquid up to a height ##H##. Find the maximum value of ##H## such that the cylinder remains in equilibrium
- Relevant Equations
- ##\vec{\tau}=\vec{r}\times\vec{F}, \sum\vec{\tau}=\vec{0}, \sum{\vec{F}}=\vec{0}##
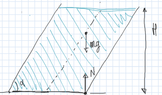
The cylinder will cease to be in equilibrium when the sum of the torques on the cylinder calculated with respect to the rightmost point of contact of the cylinder with the plane will be unbalanced. Now, the liquid is homogeneous and the cylinder has negiglible mass so the forces (normal force of the surface and gravitational force) will act on the center of mass which is in the geometric center of the figure so the lever arm of this torque with respect to said point should be ##2R-(R+\frac{L}{2}\sin(30°))=2R-(R+\frac{H}{2\sqrt{3}})=R-\frac{H}{2\sqrt{3}}##.
Now, the thing that confuses me is that these two torques have the same ##F## and the same ##r## so their algebraic sum is always ##0##.
There must be something about setting up this problem that I don't understand so I would appreciate an hint about how to reason about it.
Now, the thing that confuses me is that these two torques have the same ##F## and the same ##r## so their algebraic sum is always ##0##.
There must be something about setting up this problem that I don't understand so I would appreciate an hint about how to reason about it.