FactChecker
Science Advisor
Homework Helper
- 9,366
- 4,643
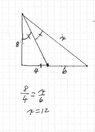
Ok.barryj said:You are wrong. The drawing is correct. You should NEVER assume things. If the drawing does not say it is a right triangle, then do not assume it is.
Should we assume that the baseline is one straight line or is there an angle at the vertex between the 4 and 6 length lines?
Should we assume that all those lines to the top meet at the same point? It looks a little like the line farthest to the right comes in at a different point.
Of course, I am being sarcastic. The point is that the easier you can make it for us, the more likely it is that you will get good help.