What happens to the force acting on the elbow with a straight bicep?

[fishes]

Homework Statement

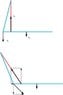
Consider a person holding their forearm horizontally in such a way that the bicep muscle, attached to the forearm at a distance of 4cm from the pivot in the elbow, is vertical. The mass of the forearm is 1 kg and the distance of the centre of mass of the forearm from the pivot is 12 cm. What is the force exerted by the bicep muscle?
(a) 117.6 N. (b) 29.4 N. (c) 9.8 N. (d) 3.27 N.

10. The person now shifts their arm so that the bicep muscle is no longer acting vertically, but the forearm is still horizontal. What happens to the force in the elbow joint?
(a) Nothing.
(b) It changes direction but not magnitude.
(c) It changes direction and decreases in magnitude.
(d) It changes direction and increases in magnitude.

Homework Equations

Net sum of torques? Clockwise torques (negative) = Counterclockwise torques (positive)

The Attempt at a Solution

So I'm pretty sure I got the first question (I chose b). I worked it out by first calculating the force acting on the center of gravity (9.8 x 1) and then using the net sum of torques to figure out the force acting on the bicep.

I'm more concerned with the second question, I know that muscle force is independent of angle but I'm a bit confused as I know that muscle angle does affect muscle fiber length which in turn affects magnitude - are magnitude and force not the same thing in this instance? I know the force of the elbow joint (fulcrum) is acting downwards when the bicep is vertical and I would have assumed that it would stay this way but this is apparently wrong as no change in direction is not an answer. Is muscle angle only independent of muscle force when it is vertical? I'm pretty lost on how to solve this question, at the moment I would assume that a change in magnitude occurs which according to this question means a change of direction occurs as well. I would probably choose (d) just because I feel like the elbow joint would have to exert extra force to make up for the missing bicep force in order to keep the forearm up?

Cheers

 

[CWatters]

What happens if you take it to extreme? eg so your whole arm is nearly horizontal. That still appears to meet the conditions specified in the problem but might be easier to visualise.

 

[fishes]

What happens if you take it to extreme? eg so your whole arm is nearly horizontal. That still appears to meet the conditions specified in the problem but might be easier to visualise.

Well I assume that the forearm centre of gravity is still exerting the same force (9.8N) and therefore the same torque which means the elbow joint + muscle need to cancel it out. I guess that once the bicep is horizontal another muscle takes over in exerting a torque to = 0 torque? I also guess that seeing as all the arm muscles can only act between the CM and the elbow joint that it is still a 3rd class lever? In that case I think that nothing happens to the force in the elbow joint and nothing happens to the direction it exerts it as the torques exerted by the CM (the CM location will change and therefore this will change the torque?) and the new muscle will change? Is that right? (A)

Also I read that while bicep force is independent of angle that due to muscle fiber length force actually does differ? Can you help explain this too me? Is there eventually an angle where the muscle fiber length cannot provide the required force to balance the torques?
Cheers

 

[BvU]

Hi fish,
If this is a physics course, you want to do a bit more physics and a little less physiology.
And I guess it is a physics course, because of the 4 cm

My tip is to make a drawing of the situation in the first question. 9.8 N downward force at the center of mass and 29.4 N upward where the biceps is attached. Biceps is vertical, so force is 29.4 N. ∑F = 0 gives elbow force.

Then a drawing for exercise 10: shift the arm (move the hand forward) such that the elbow angle is obtuse. (Case fully stretched arm is a bit awkward - I suspect the author of the exercise wants to keep the biceps doing the torque balancing)
9.8 N is still there, biceps vertical component still needs to be 29.4 N. But biceps is now pulling at an obtuse angle, so there also is a horizontal component. ∑F = 0 gives elbow force.

 

[fishes]

Hi fish,
If this is a physics course, you want to do a bit more physics and a little less physiology.
And I guess it is a physics course, because of the 4 cm

My tip is to make a drawing of the situation in the first question. 9.8 N downward force at the center of mass and 29.4 N upward where the biceps is attached. Biceps is vertical, so force is 29.4 N. ∑F = 0 gives elbow force.

Then a drawing for exercise 10: shift the arm (move the hand forward) such that the elbow angle is obtuse. (Case fully stretched arm is a bit awkward - I suspect the author of the exercise wants to keep the biceps doing the torque balancing)
9.8 N is still there, biceps vertical component still needs to be 29.4 N. But biceps is now pulling at an obtuse angle, so there also is a horizontal component. ∑F = 0 gives elbow force.

So pretty much the biceps and the CM torques/forces are still balancing one another regardless of angle (The biceps is still acting upwards and the CM is still acting down)? So because the elbow joint is acting as a fulcrum it's always acting as a downwards force with a 0 magnitude? Does that mean the answer is (A) nothing?

Thanks a lot for the help, I'm sorry it's taking this long I always take a while wrapping my head around new concepts.

 

[BvU]

You're doing fine. Keep in mind physicists brains are differently contorted.
The pictures I was thinking of:
In the top one (problem 9?) forces and torques add up to 0.

In the bottom one, F_G and the vertical component of F_B are unchanged. But because biceps is now pulling in a non-vertical direction, magnitude is bigger than only the vertical component. Elbow now has to compensate for the corresponding horizontal component too.

 

[fishes]

You're doing fine. Keep in mind physicists brains are differently contorted.
The pictures I was thinking of:
In the top one (problem 9?) forces and torques add up to 0.

In the bottom one, F_G and the vertical component of F_B are unchanged. But because biceps is now pulling in a non-vertical direction, magnitude is bigger than only the vertical component. Elbow now has to compensate for the corresponding horizontal component too.

Okay so I think I get it! The torques/forces always cancel each other out and because CM has to alway be acting downwards due to gravity the elbow joint has to change its direction to "cancel" out the now horizontal biceps? Which means that direction does change but what about magnitude? I don't really understand what you mean here: "But because biceps is now pulling in a non-vertical direction, magnitude is bigger than only the vertical component"? Are you saying the horizontal component is of a greater magnitude which means the elbow is less? In that case is the answer (B).

I really can't thank you enough by the way!

 

[haruspex]

"But because biceps is now pulling in a non-vertical direction, magnitude is bigger than only the vertical component"?

BvU is saying that the biceps still has to supply a vertical component as before (to achieve the same torque about the joint) but because of its direction it will also have a horizontal component (which does not generate any torque about the joint). Therefore the total force in the biceps is greater than before.
BvU's diagram shows you the answer to the question. You can also get there by considering what change is needed at the joint to accommodate the force change in the biceps.

 

[fishes]

BvU is saying that the biceps still has to supply a vertical component as before (to achieve the same torque about the joint) but because of its direction it will also have a horizontal component (which does not generate any torque about the joint). Therefore the total force in the biceps is greater than before.
BvU's diagram shows you the answer to the question. You can also get there by considering what change is needed at the joint to accommodate the force change in the biceps.

Ok so I assume that because the total force at the biceps is greater and because the CM's torque/force is constant that the elbow joint's force changes direction to cancel out the horizontal component of the bicep and increases in magnitude to counteract this force increase as well (Answer (d))? When you say the horizontal component doesn't generate any torque about the joint are you saying that it does produce a new torque that for another lever system which means its not counted in the torques of this system? So while the torques/forces of both the bicep are changing direction and increasing in magnitude they are the same as before when it concerns the original 3rd class lever system?

 

[haruspex]

Ok so I assume that because the total force at the biceps is greater and because the CM's torque/force is constant that the elbow joint's force changes direction to cancel out the horizontal component of the bicep and increases in magnitude to counteract this force increase as well (Answer (d))? When you say the horizontal component doesn't generate any torque about the joint are you saying that it does produce a new torque that for another lever system which means its not counted in the torques of this system? So while the torques/forces of both the bicep are changing direction and increasing in magnitude they are the same as before when it concerns the original 3rd class lever system?

The horizontal component of the force exterted by the biceps at the point of attachment acts through the joint, so generates no torque about it. Yes, it would generate a torque about points not in that line.
Btw, biceps is singular. Bicep is not a word.

 

[BvU]

And I guess it is a physics course, because of the 4 cm

I shouldn't have written it like that: looking at a bunch of images, e.g. this one the 4 cm isn't so unrealistic as I thought. Goes to show you should tread more carefully once outside your domain...