What happens when a null pointer is passed into a recursive function?

  • Context: MHB 
  • Thread starter Thread starter evinda
  • Start date Start date
Click For Summary

Discussion Overview

The discussion revolves around the behavior of a recursive function when a null pointer is passed as an argument, specifically in the context of traversing a binary tree and printing its nodes in ascending order. Participants explore the implications of calling the function with null pointers and the order of execution of commands within the recursive calls.

Discussion Character

  • Exploratory
  • Technical explanation
  • Conceptual clarification
  • Debate/contested
  • Mathematical reasoning

Main Points Raised

  • Some participants describe the recursive procedure Pr and its intended behavior when called with various nodes, including null pointers.
  • There is uncertainty about the exact problem statement and whether the goal is to predict outcomes based on the recursive calls.
  • Participants discuss the implications of executing commands after a return statement in the context of the call stack.
  • One participant suggests that the order of processing nodes should be adjusted to ensure keys are printed in ascending order, proposing a change in the traversal order.
  • Another participant explains the concept of a stack and how it relates to the execution of recursive functions, emphasizing the last-in, first-out nature of stack operations.
  • A detailed table of execution is presented to illustrate the call stack's state at various points during the execution of the recursive function.

Areas of Agreement / Disagreement

Participants express differing views on the traversal order and the implications of executing commands after a return statement. There is no consensus on the exact behavior of the algorithm following the execution of the return command, and the discussion remains unresolved regarding the optimal traversal method.

Contextual Notes

Participants highlight the importance of understanding the call stack in recursive functions, but there are limitations in the clarity of the problem statement and the assumptions about the tree structure.

Who May Find This Useful

This discussion may be useful for individuals interested in recursive algorithms, tree data structures, and the mechanics of function calls in programming languages.

evinda
Gold Member
MHB
Messages
3,741
Reaction score
0
Hello! (Nerd)

Suppose that we have this tree:

View attachment 3559

and we want to apply the following algorithm:

Code: 
Procedure Pr(pointer P){
   if (P==NULL) return;
   Pr(P->lc);
   print(P->data);
   Pr(P->rc);
}
We call the procedures [m]Pr(A), Pr(B), Pr(D), Pr(H), Pr(NULL)[/m], right?

When we run the Procedure [m]Pr(NULL)[/m], the command [m]return;[/m] is executed.
After that, what do we have to do? Do we have to execute the commands, that are under the command [m]Pr(P->lc);[/m] for [m]P->lc=H[/m] ? (Thinking)
 

Attachments

  • trr.png
    trr.png
    5.2 KB · Views: 133
Technology news on Phys.org
evinda said:
Hello! (Nerd)

Suppose that we have this tree:

View attachment 3559

and we want to apply the following algorithm:

Code: 
Procedure Pr(pointer P){
   if (P==NULL) return;
   Pr(P->lc);
   print(P->data);
   Pr(P->rc);
}
We call the procedures [m]Pr(A), Pr(B), Pr(D), Pr(H), Pr(NULL)[/m], right?

I don't know; is it part of the problem statement to make all these calls, and then predict what the outcome will be?

When we run the Procedure [m]Pr(NULL)[/m], the command [m]return;[/m] is executed.

Right.

After that, what do we have to do?

I don't know; what is the exact problem statement?

Do we have to execute the commands, that are under the command [m]Pr(P->lc);[/m] for [m]P->lc=H[/m] ? (Thinking)

When the code gets to the point where it is at H, it will call [m]Pr(H->lc)[/m]; however, that will be a null pointer, so it will return without executing the remainder of the commands in [m]Pr[/m]. Does that answer your question?
 
Ackbach said:
I don't know; is it part of the problem statement to make all these calls, and then predict what the outcome will be?
Right.
I don't know; what is the exact problem statement?

The algorithm should traverse the tree, so that the keys will be printed in ascending order.

Ackbach said:
When the code gets to the point where it is at H, it will call [m]Pr(H->lc)[/m]; however, that will be a null pointer, so it will return without executing the remainder of the commands in [m]Pr[/m]. Does that answer your question?

I wasn't sure what command the algorithm will execute, after executing the command return; .. (Thinking)
 
evinda said:
The algorithm should traverse the tree, so that the keys will be printed in ascending order.

Ok: in your mind, is G the right-most node (is it the right child or left child of C)? Because if it's the right child, and you need to print in ascending order, then you should process right child, node, then left child - the opposite of the order you have.

I wasn't sure what command the algorithm will execute, after executing the command return; .. (Thinking)

When the return is executed, then that call of [m]Pr[/m] is done executing, and will leave the stack, and you'll go back to the parent's instance of [m]Pr[/m].
 
Ackbach said:
Ok: in your mind, is G the right-most node (is it the right child or left child of C)? Because if it's the right child, and you need to print in ascending order, then you should process right child, node, then left child - the opposite of the order you have.
Oh yes, you are right! (Blush) So, should it be like that?

Code: 
Procedure Pr(pointer P){
   if (P==NULL) return;
   Pr(P->rc);
   print(P->data);
   Pr(P->lc);
}

Ackbach said:
When the return is executed, then that call of [m]Pr[/m] is done executing, and will leave the stack, and you'll go back to the parent's instance of [m]Pr[/m].

So, the procedures [m]Pr(A),Pr(C),Pr(G),Pr(NULL)[/m] will be executed, then the number 42 will be printed. Then, the procedure [m] Pr(NULL)[/m] will be called and the command return; will be executed, right? (Thinking) And, what happens after that? :confused:
 
evinda said:
Oh yes, you are right! (Blush) So, should it be like that?

Code: 
Procedure Pr(pointer P){
   if (P==NULL) return;
   Pr(P->rc);
   print(P->data);
   Pr(P->lc);
}

Yes, at least that's correct in pseudocode. The exact syntax you'll need to make work in whatever language you're using.

So, the procedures [m]Pr(A),Pr(C),Pr(G),Pr(NULL)[/m] will be executed, then the number 42 will be printed. Then, the procedure [m] Pr(NULL)[/m] will be called and the command return; will be executed, right? (Thinking)

Exactly right. Now the [m]G[/m] node has been fully processed, and the [m]Pr(G)[/m] call to the function will finish executing. Then the program gets rid of that instance of [m]Pr[/m] from the stack, and continues executing the [m]Pr(C)[/m] instance. It's finished the right child, so now it does what?
 
Ackbach said:
Yes, at least that's correct in pseudocode. The exact syntax you'll need to make work in whatever language you're using.
Exactly right. Now the [m]G[/m] node has been fully processed, and the [m]Pr(G)[/m] call to the function will finish executing. Then the program gets rid of that instance of [m]Pr[/m] from the stack, and continues executing the [m]Pr(C)[/m] instance. It's finished the right child, so now it does what?

We will have something like that, right?

View attachment 3562

After that, why do we execute the commands [m] print(C->data)[/m] and [m]Pr(C->lc)[/m]?
If there were also other commands, after the command [m]Pr(P->lc)[/m], would they be executed for G or would the [m]G[/m] node be again fully processed? (Thinking)
 

Attachments

  • call.png
    call.png
    1.2 KB · Views: 114
evinda said:
We will have something like that, right?

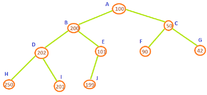
View attachment 3562

After that, why do we execute the commands [m] print(C->data)[/m] and [m]Pr(C->lc)[/m]?
If there were also other commands, after the command [m]Pr(P->lc)[/m], would they be executed for G or would the [m]G[/m] node be again fully processed? (Thinking)

It seems to me that the missing concept in your understanding is the idea of a stack. The basic idea of a stack is simple: last in, first out. That is, the last thing you put on the stack is the first thing you take off it. Think of one of those cafeteria tray stacks with the springs under them, or like what some restaurants have with springs underneath plates. "Pushing" is the act of putting something on the stack, and "popping" is the act of taking something off the stack. A stack is to be contrasted with a linked list, where the first thing you put in the last is the first thing you would take off the list (first in, first out).

Now then, when you call a function in a language, all sorts of things happen, but one thing that happens is that there is a place in the computer where the execution control is (what's going to be executed next). This is the "call stack". It tells you what will execute next.

When you use a recursive function like [m]Pr[/m], the call stack is absolutely essential to understanding what's going to happen next. I'm going to see if I can illustrate with a little table of execution here. The code will be on the left, and the stack will be on the right. The "top" of the stack will be to the right, and the Call Stack State will be what the call stack looks like after the corresponding code to the left finishes executing. Also, you have to keep track of which function instance is currently running, so I'll do that with dot notation. "Pr(A).statement" means that "statement" is executing in the "Pr(A)" instance.

[table="width: 700, align: left"]
[tr]
[td]Code Executing [/td]
[td]Call Stack State (top is to the right)[/td]
[/tr]
[tr]
[td]Pr(A)[/td]
[td]Pr(A) (pushing Pr(A) onto the stack)[/td]
[/tr]
[tr]
[td]Pr(A).(A==NULL) False[/td]
[td]Pr(A)[/td]
[/tr]
[tr]
[td]Pr(A).Pr(C)[/td]
[td]Pr(A), Pr(C) (pushing Pr(C) onto the stack)[/td]
[/tr]
[tr]
[td]Pr(C).(C==NULL) False[/td]
[td]Pr(A), Pr(C)[/td]
[/tr]
[tr]
[td]Pr(C).Pr(G)[/td]
[td]Pr(A),Pr(C),Pr(G) (pushing Pr(G) onto the stack)[/td]
[/tr]
[tr]
[td]Pr(G).(G==NULL) False[/td]
[td]Pr(A), Pr(C),Pr(G)[/td]
[/tr]
[tr]
[td]Pr(G).Pr(G->rc) [/td]
[td]Pr(A),Pr(C),Pr(G),Pr(G->rc) (pushing Pr(G->rc) onto the stack)[/td]
[/tr]
[tr]
[td]Pr(G->rc).(G->rc==NULL) True[/td]
[td]Pr(A),Pr(C),Pr(G),Pr(G->rc)[/td]
[/tr]
[tr]
[td]Pr(G->rc).return [/td]
[td]Pr(A),Pr(C),Pr(G) (popping Pr(G->rc) off the stack) [/td]
[/tr]
[tr]
[td]Pr(G).print(G->data) (42) [/td]
[td]Pr(A),Pr(C),Pr(G)[/td]
[/tr]
[tr]
[td]Pr(G).Pr(G->lc) [/td]
[td]Pr(A),Pr(C),Pr(G),Pr(G->lc) (pushing Pr(G->lc) onto the stack)[/td]
[/tr]
[tr]
[td]Pr(G->lc).(G->lc==NULL) True[/td]
[td]Pr(A),Pr(C),Pr(G),Pr(G->lc)[/td]
[/tr]
[tr]
[td]Pr(G->lc).return[/td]
[td]Pr(A),Pr(C),Pr(G) (popping Pr(G->lc) off the stack)[/td]
[/tr]
[tr]
[td]Pr(G).} (end of routine) [/td]
[td]Pr(A),Pr(C) (popping Pr(G) off the stack)[/td]
[/tr]
[tr]
[td]Pr(C).print(C->data) (50) [/td]
[td]Pr(A),Pr(C)[/td]
[/tr]
[tr]
[td]Pr(C).Pr(F) [/td]
[td]Pr(A),Pr(C),Pr(F) (pushing Pr(F) onto the stack)[/td]
[/tr]
[tr]
[td]Pr(F).(F==NULL) False[/td]
[td]Pr(A),Pr(C),Pr(F)[/td]
[/tr]
[tr]
[td]Pr(F).Pr(F->rc) [/td]
[td]Pr(A),Pr(C),Pr(F),Pr(F->rc) (pushing Pr(F->rc) onto the stack)[/td]
[/tr]
[tr]
[td]etc.[/td]
[td][/td]
[/tr]
[/table]

Hopefully, if you have your latest version of your code, and the tree itself in front of you, and you compare this table of execution with those carefully, it will help you to see what's going on. Does this help?

You really have to have multiple levels of abstraction in your mind simultaneously in order to understand recursion.
 
I haven't understood why we finish with the node G and continue with the node C.. (Worried)
Because of the execution of [m]Pr(G->lc)=Pr(NULL)[/m] or because of the fact that there are no other commands after the command [m]Pr(G->lc)[/m] ? :confused:
 
  • #10
evinda said:
I haven't understood why we finish with the node G and continue with the node C.. (Worried)
Because of the execution of [m]Pr(G->lc)=Pr(NULL)[/m] or because of the fact that there are no other commands after the command [m]Pr(G->lc)[/m] ? :confused:

The second. We process [m]Pr(G->lc)[/m], but that is a null pointer. Since we have processed the left child, and that's the last command in the recursive function, then [m]Pr(G)[/m] finishes executing, and gets popped off the call stack. This is represented in my table somewhat awkwardly by the [m]Pr(G).}[/m] line.
 

Similar threads

MHB Deleting Leaf Nodes from an Ordered Binary Tree
  • · Replies 2 ·
Replies
2
Views
2K
MHB What is the Time Complexity of These Binary Search Tree Functions?
  • · Replies 3 ·
Replies
3
Views
2K
MHB Is my AVL-tree height finding method correct?
  • · Replies 1 ·
Replies
1
Views
2K
MHB In which case will the command be executed?
  • · Replies 7 ·
Replies
7
Views
3K
MHB Destroying a Planetary System: Analyzing Solid's Destruction Function
  • · Replies 2 ·
Replies
2
Views
2K
MHB Collision of Planets: FF & AS Destruction
  • · Replies 1 ·
Replies
1
Views
2K
MHB What Are the Complexity and Operations of a Static Queue?
  • · Replies 9 ·
Replies
9
Views
3K
Python RecursionError at a place where I have defined no recursive function
  • · Replies 17 ·
Replies
17
Views
3K
MHB Constructing a Star System with O(1) Complexity
  • · Replies 20 ·
Replies
20
Views
5K
MHB List that contains only the elements of the one of the two given lists
  • · Replies 6 ·
Replies
6
Views
2K