What is a Photon? - Physics Basics Explained

[tionis]

Well, I never understood why I had to learn "old-fashioned quantum theory" and then had to unlearn it (and the QM1 lecture is usually taught in the 4th-5th semester and not only in graduate school).

I suppose the ''old-fashioned'' way eases you into the new like bhobba says, but just the thought of having to wait all those years to learn the most accurate picture is daunting, but I look forward to it. Must be nice to be you guys and have all that knowledge.

 

[bhobba]

Well, I never understood why I had to learn "old-fashioned quantum theory" and then had to unlearn it (and the QM1 lecture is usually taught in the 4th-5th semester and not only in graduate school).

I have said it before, and will say it again, teaching QM along the lines of the following is much more rational:
http://www.scottaaronson.com/democritus/lec9.html

Thanks
Bill

 

[bhobba]

I suppose the ''old-fashioned'' way eases you into the new like bhobba says, but just the thought of having to wait all those years to learn the most accurate picture is daunting, but I look forward to it. Must be nice to be you guys and have all that knowledge.

Sometimes you need to do it the learn a half truth then unlearn it way, and sometimes not. In QM a lot of it has to do with the semi historical way its usually presented and could be replaced with something much more rational.

My view of physics, based heavily on symmetry, was very hard won from reading bits here and there and fitting it together.

In that journey the following book was crucial:
https://www.amazon.com/dp/0750628960/?tag=pfamazon01-20

As one reviewer said:
'If physicists could weep, they would weep over this book. The book is devastingly brief whilst deriving, in its few pages, all the great results of classical mechanics. Results that in other books take take up many more pages. I first came across Landau's mechanics many years ago as a brash undergrad. My prof at the time had given me this book but warned me that it's the kind of book that ages like wine. I've read this book several times since and I have found that indeed, each time is more rewarding than the last.

The reason for the brevity is that, as pointed out by previous reviewers, Landau derives mechanics from symmetry. Historically, it was long after the main bulk of mechanics was developed that Emmy Noether proved that symmetries underly every important quantity in physics. So instead of starting from concrete mechanical case-studies and generalising to the formal machinery of the Hamilton equations, Landau starts out from the most generic symmetry and dervies the mechanics. The 2nd laws of mechanics, for example, is derived as a consequence of the uniqueness of trajectories in the Lagragian. For some, this may seem too "mathematical" but in reality, it is a sign of sophisitication in physics if one can identify the underlying symmetries in a mechanical system. Thus this book represents the height of theoretical sophistication in that symmetries are used to derive so many physical results.

The difficulty with this approach, and the reason why this book is not a beginner's book, is that to the follow symmetric arguments, one really has to have already mastered vector calculus.'

And that is the whole issue. In order to get to the deep and powerful beauty of physics one must have a certain amount of mathematical maturity - you must be eased into it.

Thanks
Bill

 

[Andy Resnick]

In answering a question in general physics I came across the following which explains at a reasonably basic level what a photon is, spontaneous emission etc at the level of basic QM with a bit of math:
http://www.physics.usu.edu/torre/3700_Spring_2015/What_is_a_photon.pdf

This is also not the entirely correct way to view photons, I'm sorry to say. First of all as massless quanta with spin $1$ there's no position operator. So the naive uncertainty relation, valid for massive particles, doesn't make sense to begin with. For a review, see
http://arnold-neumaier.at/physfaq/topics/position.html

I came to quantum optics via 'second quantization' as per bhobba's reference, but have recently become aware of the deficiencies in that approach:

http://www.worldscientific.com/worldscibooks/10.1142/9251

Not being a mathematician, please forgive any mis-statements- I am interested in what the above authors have to say, but don't fully understand what they are saying and so comments are appreciated. As best I can tell, they claim that:

1) The Fock representation is only defined on simply-connected spaces. This is sufficient for many optical cavities, but there are more complex topologies: ring-shaped and bowtie-shaped cavities, branching networks, etc., and the Fock space may not be applicable to those.

2) The field operators live in an infinite dimensional space, and many of the operators are unbounded.

The authors seem to have developed a completely different approach, based on algebraic quantization.

Unfortunately for me, I am trying to parse statements like "The one-photon Hilbert space is given by H^T=P^TL²(Λ,ℂ³)" and "As the C*-algebra of observables we have chosen the Weyl algebra W(E^T, ħ Im(.|.)). The free, diagonalized transversal Maxwell dynamics is given by the one-parameter group of Bogoliubov *-automorphisms α_t^free, t∈ℝ, α_t^free(W^ħ(f))=W^ħ(e^itS/ħf), ∀f∈E^T".

It's slow going...

 

[vanhees71]

Wow, that I can imagine. I guess all the physics is buried under tons of complicated mathematical symbols ;-)). As far as I know, there's no rigorous QED anyway. So perhaps, it's simpler and sufficient to use a standard quantum optics textbook like Scully&Zubairy or Mandel&Wolf.

 

[exponent137]

Hi Guys and Gal's

In answering a question in general physics I came across the following which explains at a reasonably basic level what a photon is, spontaneous emission etc at the level of basic QM with a bit of math:
http://www.physics.usu.edu/torre/3700_Spring_2015/What_is_a_photon.pdf

IMHO its much better than the usual misleading hand-wavey stuff and even if you don't follow the math would allow a general gist to be had.

Thanks
Bill

The passage from both equations for $A_k$ in page 6 is not clear to me. (Last eq. and one before.) One equation is dependent of $t$ and another is not dependent on $t$. Is the last equation only for the amplitude? What means non-quantum $a_{k \sigma}$? Is it built from real and imaginary parts? What they means physically?

 

[bhobba]

The passage from both equations for $A_k$ in page 6 is not clear to me. (Last eq. and one before.) One equation is dependent of $t$ and another is not dependent on $t$. Is the last equation only for the amplitude? What means non-quantum $a_{k \sigma}$? Is it built from real and imaginary parts? What they means physically?

Its simply the general solution to the wave equation - a bit of partial differential equations theory is used. The explicit time dependence is subsumed into the fact its a wave of a certain frequency so doesn't need to be stated - its subsumed into k. The two components are related to polarization the details of which I only have dim memories of from my study of Maxwell's Equations ages ago - but I did find the following that gives the gory detail if you are interested:
http://course.ee.ust.hk/elec342/notes/lecture3_electromagnetics-1.pdf

Its in terms of complex numbers. To get the quantum equation you replace them by operators.

If you want the full mathematical detail you can find it in Chapter 6 of Von Neumann's Mathematical Foundations.

Thanks
Bill

 

[edguy99]

Again, these statements are very misleading, not only but particularly for photons. One should emphasize that one cannot think about quanta, particularly massless quanta like the photon, in terms of classical fields ("waves") or particles. There is no wave-particle dualism, there is no position operator for photons and thus you cannot define in a reasonable way what a photon's position is. All these ideas are gone from modern physics for more than 90 years now!

The thinking of George Box, one of the great statistical minds of the 20th century, who wrote that “essentially, all models are wrong, but some are useful” applies here:

Now it would be very remarkable if any system existing in the real world could be exactly represented by any simple model. However, cunningly chosen parsimonious models often do provide remarkably useful approximations. For example, the law PV = RT relating pressure P, volume V and temperature T of an “ideal” gas via a constant R is not exactly true for any real gas, but it frequently provides a useful approximation and furthermore its structure is informative since it springs from a physical view of the behavior of gas molecules.

For such a model there is no need to ask the question “Is the model true?”. If “truth” is to be the “whole truth” the answer must be “No”. The only question of interest is “Is the model illuminating and useful?”.
​

The original article posted here speaks of photons as harmonic oscillators. A very important point in understanding the basic mathematics on how to calculate energy and the concept relating wavelength to energy. Maxwells equations are very important to introduce the concept of the electrical axis of a photon. The QM idea of Jones vectors and Dirac bracket notation, are much easier to understand after seeing the electrical axis on a picture or model of Maxwells equations.

There is a need for photon representation that starts out a little easier then "The one-photon Hilbert space is given by HT=PTL2(Λ,ℂ3)", but provides a a basis for proper understanding into the principle properties of a photon.

 

[DrChinese]

The thinking of George Box, one of the great statistical minds of the 20th century, who wrote that “essentially, all models are wrong, but some are useful” applies here:

Now it would be very remarkable if any system existing in the real world could be exactly represented by any simple model. However, cunningly chosen parsimonious models often do provide remarkably useful approximations. For example, the law PV = RT relating pressure P, volume V and temperature T of an “ideal” gas via a constant R is not exactly true for any real gas, but it frequently provides a useful approximation and furthermore its structure is informative since it springs from a physical view of the behavior of gas molecules.

For such a model there is no need to ask the question “Is the model true?”. If “truth” is to be the “whole truth” the answer must be “No”. The only question of interest is “Is the model illuminating and useful?”.
​

Great words, sadly this point is often missed in basic discussions. The "answer" can change according to the point being made. All theories are models of some type, and may be judged on their utility. Some are more useful than others. For example, even Newtonian gravity is useful to the manufacturer of a scale.

 

[vanhees71]

Well, "old quantum theory" is not among the useful theories. That's why it was developed further in modern quantum theory!

 

[Fooality]

Hold on.

This is a well known issue.

You are given half truths to start with that gradually gets corrected as you learn more. It happens in physics, and expecially QM, all the time eg the wave particle duality. Feynman commented on it - he didn't like it - but couldn't see any way around it.

Its just the way things are.

The reason I posted the link is it should be accessible to people who have done a proper first course in QM. Its not the last word - its just better than the usual hand wavy stuff about what photons are.

Thanks
Bill

I just want to respond that I love posts that make QM approachable to non physics people. I am a computer science guy, and some very important problems in AI, augmented reality, VR and more can be tackled once a good, computationally affordable approximate simulation of the behavior of light can be made... But at present, it doesn't exist. The natural path should be to look at the best physics of light, (QM) to draw some inspiration for computationally cheap approximations of these systems that might scale. But its very difficult for a physics outsider to get a clue in QM. These articles that offer approximate explanations are therefore really useful to someone in my place, as I'm driven largely by curiosity and seeking approximations, ratjer than a professional career in physics.

 

[vanhees71]

Well, I don't think that QED is the appropriate approach to optics for computer simulations. I guess a great deal is already sufficiently well described by ray optics.

 

[A. Neumaier]

some very important problems in AI, augmented reality, VR and more can be tackled once a good, computationally affordable approximate simulation of the behavior of light can be made... But at present, it doesn't exist. The natural path should be to look at the best physics of light

For practical purposes, the best physics of light is still geometric optics unless you want to be able to reproduce diffraction phenomena. In that case you need the Maxwell equations. But quantum mechanics is needed only if you want to reproduce microscopic behavior, which would be far too expensive to simulate, and probably has no effect at all on the visual quality of what you compute.

 

[edguy99]

For practical purposes, the best physics of light is still geometric optics unless you want to be able to reproduce diffraction phenomena. In that case you need the Maxwell equations. But quantum mechanics is needed only if you want to reproduce microscopic behavior, which would be far too expensive to simulate, and probably has no effect at all on the visual quality of what you compute.

Certainly ray tracing provides a good model for things like telescope lenses or prisms. For behaviors of photons like diffraction or anything that depends on the wavelength of light, the harmonic oscillator provides a great model. For example, a harmonic oscillator that is periodic in time allows you to model interference and reinforcement. Modeling an oscillating photon makes it easy for the animator to illustrate wave reinforcement and wave interference. Consider how oscillators can model reinforcement and interference for photons caught in a small cavity (click here) or how interference depends on how far the photon travels relative to other photons in a model of a Michelson interferometer (click here).

 

[Andy Resnick]

<snip>

There is a need for photon representation that starts out a little easier then "The one-photon Hilbert space is given by HT=PTL2(Λ,ℂ3)", but provides a a basis for proper understanding into the principle properties of a photon.

Sure- and this is one reason why I learned the canonical quantization scheme (harmonic oscillators and Hermite polynomials, Fock and Glauber states, etc.) oh so many years ago, and why I teach that particular content to my students today.

For myself, however, I like to explore the subject a little deeper because the 'simpler' representation does not correspond all that well to classical E&M- the number of photons does not correspond to the intensity of the field, for example.

 

[vanhees71]

The number of photons is a tricky quantity anyway. Think about its Lorentz invariance! It's always good to let one guide by classical electrodynamics, which leads you to define the intensity of the field as its energy density, which is a well-defined covariant quantity (as 00 component of the symmetric energy-momentum tensor of the em. field).

 

[Fooality]

For practical purposes, the best physics of light is still geometric optics unless you want to be able to reproduce diffraction phenomena. In that case you need the Maxwell equations. But quantum mechanics is needed only if you want to reproduce microscopic behavior, which would be far too expensive to simulate, and probably has no effect at all on the visual quality of what you compute.

Thanks for your reply, and vanhees. Geometric optics has produced some really good simulations, (called ray tracing, ray marching etc) but they are also really expensive. There's big demand for shortcuts that can produce comparable results. My curiosity to look into QM came from asking the simple question of what light is really doing at the deepest level with hope of finding some inspiration for approximations. I haven't found any, but its still really interesting to hear these somewhat simplified versions of what's going on, as offered to the public by Feynman and Susskind, and some people here. Its especially important because I have never found a subject before where Googling it to learn about it returns so much pseudo scientific BS from people who don't really know what their talking about! Its a good thing to keep the public informed.

 

[A. Neumaier]

Geometric optics has produced some really good simulations, (called ray tracing, ray marching etc) but they are also really expensive. There's big demand for shortcuts that can produce comparable results.

But geometric optics is already a shortcut to quantum optics and the Maxwell equations - so for further shortcuts you need to go into the other direction - simplifying geometric optics. This has no longer anything to do with quantum physics!

 

[fluidistic]

The number of photons is a tricky quantity anyway. Think about its Lorentz invariance! It's always good to let one guide by classical electrodynamics, which leads you to define the intensity of the field as its energy density, which is a well-defined covariant quantity (as 00 component of the symmetric energy-momentum tensor of the em. field).

Hmm what do you mean by this comment? That the number of photons might not be a Lorentz invariant?
Here's a proof stating that it is: https://physics.stackexchange.com/q...er-of-photons-of-a-system-a-lorentz-invariant , is it wrong?

 

[vanhees71]

I'm not sure about the derivation in stackexchange. I'd have to analyze it with some detail. It's not clearly stated how the states are normalized, etc. The point is that there's no conserved current for photons and thus, it's not so simple to define a Lorentz invariant number-like quantity. What you can define is of course energy and momentum densities which fulfill continuity equations with their corresponding currents (or simply use the energy-momentum tensor which fulfills $\partial_{\mu} \Theta^{\mu \nu}=0$), and this shows that energy and momentum properly transform as a four vector and thus are covariant.

 

[Fooality]

But geometric optics is already a shortcut to quantum optics and the Maxwell equations - so for further shortcuts you need to go into the other direction - simplifying geometric optics. This has no longer anything to do with quantum physics!

Yes, and there are many attempts to do just that people are working on. My curiosity about QM came from the fact that the concept of rays is awkward for computation. I wondered if there was some other view, maybe waves or something else as far as a simplified approximation that might be out there. Its really not important unless its interesting to you. Maybe I'm curious because of quantum computers, or quantum limits in chip manufacture, or anything else. QM is and will be a big part of the computer world. My only real point is I for one like the simplified views people offer...

 

[vanhees71]

Well, to any complicated problem there's always a simple answer, which, however, is usually wrong ;-)).

 

[lox_and_whiskey]

Great article. No better way to introduce photons then talking about harmonic oscillators. A simple harmonic oscillator is anything with a linear restoring potential. Simple things like a spring, or a string with tension, or a wave. Erwin Schrödinger described mathematically how a harmonic oscillator stores energy and how to calculate how much energy it stores.

For the photon, the value of this restoring potential is the Planck constant (h). Planck’s constant, relates the amount of energy stored in a photon to its wavelength (λ). Planck’s constant tells you the amount of time it takes the photon to undergo one cycle of whatever its doing given that the photon has a specific amount of energy. The equation E for energy = h / λ, tells us that a photon with low energy will take much longer to complete one cycle of the wave then a photon with high energy.

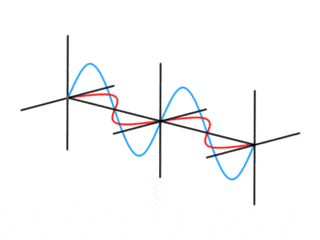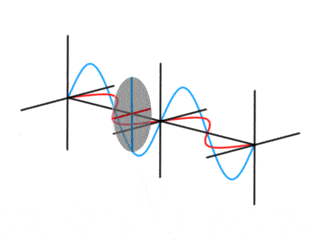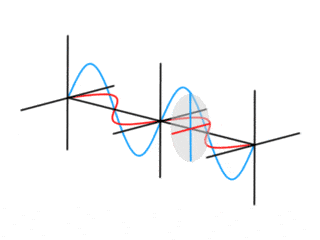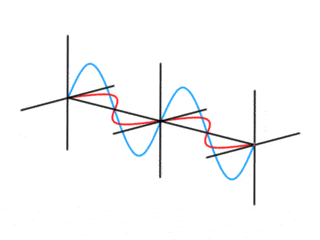
My favorite model of a photon as a harmonic oscillator is as an expanding and contracting ball of energy flying though the air. It immediately lends understanding to the particle and wave nature of the photon. A photon of a specific wavelength has a specific energy. The properties of a photon change periodically over time and distance depending on the wavelength. High energy photons oscillate very fast and store a lot of energy, low energy photons oscillate very slowly. Photons can be in the same place at the same time, sometimes reinforcing each other, sometimes cancelling each other out and it looks like there are no photons at all. The uncertainty principle: ΔxΔp ≥ h/4π falls from this. The photon is either big affecting a wide area, or it’s tiny and only affecting one small area, it cannot be both at the same time. The importance of visualizing the photon as a harmonic oscillator cannot be overstated.

That's a very nice explanation.

As a general question i'd be curious if something were elaborated on, is there any difference between vacuum and two photons canceling each other out?

 

[vanhees71]

Two photons cannot simply cancel out in the vacuum due to energy-momentum conservation. You can have (theoretically) processes like inverse pair annihilation, i.e., $\gamma \gamma \rightarrow \mathrm{e}^+ \mathrm{e}^-$.

 

[A. Neumaier]

waves or something else as far as a simplified approximation

waves are not a simplification but a computational burden as they must be computed at every point in space and not only (as rays) where they meet a surface. Thus it is far more expensive to work with waves than with rays. Forget quantum mechanics for image rendering. Also forget quantum computing (at least for the next 10 years) - at present, they cannot even sort a list of 1000 items in an acceptable time, even in a very generous view.

 

[A. Neumaier]

You can have (theoretically) processes like inverse pair annihilation,

But only at energies high enough to convert it into the mass of two electrons. This requires a very large intensity.

 

[vanhees71]

Indeed, I've somewhere read that people are after an experimental verification for this process (in lowest order perturbation theory a pure QED process), but as far as I know, it's not yet observed.

 

[maline]

My favorite model of a photon as a harmonic oscillator is as an expanding and contracting ball of energy flying though the air. It immediately lends understanding to the particle and wave nature of the photon

Sorry, but this is just wrong- not in the sense of "oversimplified" like the models George Box referred to, but simply unrelated to reality. The conception of a "photon" that "flies through the air" is presumably a classical electromagnetic wave packet. This is, I think, acceptable as a (very) oversimplified model. But waves do not "expand and contract as they move"! The motion of a wave consists precisely of "following" a peak of the wave, while the field & energy values at the peak are constant (or diminishing if the wave spreads out).
A good way to think of a wave is as a chain of oscillators (say springs, connected end to end, with small frictionless masses between each pair). When one is "energized" (compressed) it can relax by passing the energy on to the next spring. This makes a "ripple" that passes along the chain. If one spring is moving harmonically, the next one will also oscillate with a slight delay, and you get a moving sine wave. There is no one oscillator that moves.

 

[Fooality]

waves are not a simplification but a computational burden as they must be computed at every point in space and not only (as rays) where they meet a surface. Thus it is far more expensive to work with waves than rays...

[Mentor's note: A digression on quantum computing has been moved into its own thread: https://www.physicsforums.com/threads/status-of-quantum-computing.880521/]

I don't know what you mean here. With classical waves, like audio, its pretty straightforward to compute their value along a surface some distance from the source.

You're shooing me away from QM, but I don't see the problem with looking into it. For instance, in the ray tracing model tells me a photon moves in a straight line, and if it hits, say, a mirror, it bounces off at the angle of incidence every time. But when I listen to Feynman's talks, he says that point it hit in the mirror only emerges as a probability, given by his path integral. So 'rays' only probably exist, right? If they were a computationally graceful lie, I'd run with it. But they're truly not. Read the second paragraph of the wiki article on angle of incidence for one of the many reasons. Its not the fact its a lie that bothers me, its the bizarre idea that its the ONLY lie which approximates the truth that does.

Referring to to the best scientific model for a system, when seeking to simulate it, just doesn't strike me as a far out idea.

 

[A. Neumaier]

Referring to to the best scientific model for a system, when seeking to simulate it

Why don't you then start with the standard model? This is the best scientific modle for reality on Earth that we currently have. You'll find that, to caclulate anything of interest to you, you need to climb up the standard ladder of approximations until you reach ray optics and even that - the highest rung of the ladder, simpler than the Maxwell equations - is not fast enough, as you complained. There is no use at all starting at very accurate but expensive descriptions when the simpler (and still fairly accurate) models are already too slow.