What is Electrical Field in a Closed surface with no charge

[Prateek Kumar Jain]

As per the Gauss Law , Net Flux Electric Field through a closed Surface (Gaussian Surface) is zero if no charge is enclosed.

As per the definition of the Electrical Flux = Electrical Field Intensity dot product Area Vector i.e. Closed Integral of E.S

If Electrical Flux is zero then as per the definition of Electric Flux above , Electric Field intensity through the Gaussian Surface should also be zero, which is not so as shown in the figure below

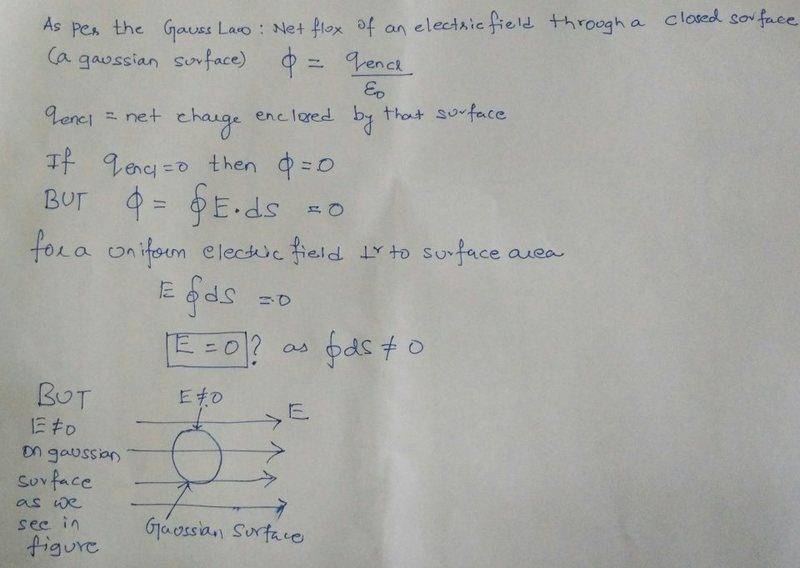
Please clarify why the two results are opposite and which one is correct.

 

[Dale]

If Electrical Flux is zero then as per the definition of Electric Flux above , Electric Field intensity through the Gaussian Surface should also be zero,

This is not necessarily correct. A zero net flux could mean that the field is zero everywhere, or it could mean that it points inward on one half and outward on the other half.

Usually you need some more information, like symmetry, in order to make the inference from 0 net flux to 0 field.

 

[Delta2]

In your hand writing text you do the mistake in the line $E\oint dS=0$ this is not correct in your example of the sphere inside a uniform field E. The field E is not always perpendicular to the surface element and even when it is, it doesn't have the same direction with the direction of the normal of the surface element.

What happens in your example is that the flux at the left half of the sphere is negative and cancels the flux at the right half which is equal but positive.(remember the positive direction for the normal to the surface element is the one that points outwards from the closed surface.)

 

[Prateek Kumar Jain]

I agree and now I understand my mistake that I was considering Electric Field to be normal to each and every surface element of the Sphere which is not so. Hence Electric Field at the Gaussian surface (Sphere) will not be zero.

Thank you for your explanation Mr. Dale and Delta