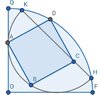
What is the area of square ABCD with OQ = OF = 6?
Click For Summary
SUMMARY
The area of square ABCD is definitively calculated to be 12 square units, based on the given conditions where OQ = OF = 6. Utilizing coordinate geometry, the midpoint M of the semicircle HK is established, leading to the derivation of the variables t and u. The relationship between these variables confirms that the distance AB equals t, thus validating the area calculation as t² = 12.
PREREQUISITES- Coordinate geometry principles
- Understanding of semicircles and their properties
- Basic algebra for solving quadratic equations
- Knowledge of geometric properties of squares
- Explore advanced coordinate geometry techniques
- Study properties of semicircles and their applications in geometry
- Learn about quadratic equations and their solutions in geometric contexts
- Investigate geometric proofs for area calculations of polygons
Mathematicians, geometry students, educators, and anyone interested in applying coordinate geometry to solve area problems in polygons.
Similar threads
High School
Area of Overlapping Squares
- · Replies 10 ·
- · Replies 1 ·
- · Replies 1 ·
- · Replies 7 ·
- · Replies 4 ·
- · Replies 6 ·
- · Replies 5 ·