What is the area of the region bounded by the given curves and lines?

[Monoxdifly]

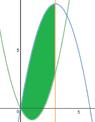
The area of the region $$y=-x^2+6x$$, $$y=x^2-2x$$, Y-axis, and the line x = 3 is ...
A. 16 unit area
B. 18 unit area
C. $$\frac{64}{3}$$ unit area
D. 64 unit area
E. 72 unit area

Sorry I couldn't post the graph, but I interpreted it as $$\int_0^3(-x^2+6x-x^2+2x)dx-\int_0^2(x^2-2x)dx$$ and got $$\frac{31}{3}$$. Did I misinterpret the graph?

 

[MarkFL]

Let's first look at the bounded region:

View attachment 7972

And so the area is:

$$A=\int_0^3 (-x^2+6x)-(x^2-2x)\,dx=2\int_0^3 -x^2+4x\,dx=2\left[-\frac{x^3}{3}+2x^2\right]_0^3=2(18-9)=18$$

I don't see where your second integral comes from, but the first one (on the left) is correct.

 

[Monoxdifly]

My second integral came from the area under the X-region.

 

[MarkFL]

My second integral came from the area under the X-region.

That's already included in the "top curve minus the bottom curve." :)

 

[Monoxdifly]

Why, though? I thought the region below the X-axis should be negative integral.

 

[MarkFL]

Why, though? I thought the region below the X-axis should be negative integral.

You're being asked to find an area, and in essence, you're doing so by adding up a bunch of vertical lines, the length of which are determined by the distance from the top curve to the bottom curve. This is found by taking the $y$-coordinate of the top curve and subtracting the $y$-coordinate of the bottom curve.