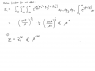aaaa202
- 1,144
- 2
Homework Statement
See the attached picture
Homework Equations
The equations given should be the relevant ones.
The Attempt at a Solution
I feel I got a bad intuition and understanding of this problem. I could eliminate T in favor of S and then express x and T by U and S. Is this how its supposed to be done? I don't think so, because I wonna use the information that the wall slides without friction at some point. Anyone have an idea what to do?
Also I don't agree with the expression for the entropy given. If you do a phase space integral to find the partition function you have to integrate over the walls position too, so you end up with an expression where T is not just raised to the power of 3N/2 but more (after all the 3N/2 is just an ideal gas in a container with fixed walls). Don't YOU agree on this?