What is the expected time difference for two posts in the same minute?

[anemone]

If $x, y, z$ are real numbers such that $x+y+z=6$, $xy+yz+xz=9$, find the sum of all possible values of the expression $\lfloor x\rfloor+\lfloor y\rfloor+\lfloor z\rfloor$.

 

[I like Serena]

Re: Evaluate ⌊x⌋+⌊y⌋+⌊z⌋

If $x, y, z$ are real numbers such that $x+y+z=6$, $xy+yz+xz=9$, find the sum of all possible values of the expression $\lfloor x\rfloor+\lfloor y\rfloor+\lfloor z\rfloor$.

Spoiler

Since the floor of a real number is at most, but not quite, 1 point lower than the original number, it follows that:
$$3 < ⌊x⌋+⌊y⌋+⌊z⌋ \le 6$$
$$4 \le ⌊x⌋+⌊y⌋+⌊z⌋ \le 6$$

Working out the equations for instance for x=0, x=ε, and x=1-ε (where ε > 0 is an arbitrary small number), shows that the numbers 4, 5, and 6 are all possible.
Therefore the sum of all possible values of ⌊x⌋+⌊y⌋+⌊z⌋ is 4+5+6=15.

 

[Opalg]

Re: Evaluate ⌊x⌋+⌊y⌋+⌊z⌋

[sp]Let $k=xyz$. The polynomial with roots $x,y,z$ is then $\lambda^3 - 6\lambda^2 + 9\lambda - k.$

View attachment 1647​

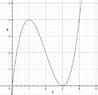
You can see from the graph that the only values of $k$ for which the equation $k = \lambda^3 - 6\lambda^2 + 9\lambda$ has three real roots are $0\leqslant k\leqslant4.$ As $k$ increases from $0$ to $4$, we can tabulate the values of the roots as follows, where the $+$ and $-$ subscripts mean addtition or subtraction of a small amount (less than $1/2$). $$\begin{array}{c|c|c|c}k&x,y,z & \lfloor x\rfloor,\, \lfloor y\rfloor,\, \lfloor z\rfloor & \lfloor x\rfloor+\lfloor y\rfloor+\lfloor z\rfloor \\ \hline 0& 0,\,3,\,3 &0,\,3,\,3 & 6 \\ 1 & 0_+,\,3_-,\,3_+ & 0,\,2,\,3 & 5 \\ 2 & 0_+,\,2,\,4_- & 0,\,2,\,3 & 5 \\ 3 & 0_+,\,2_-,\,4_- & 0,\,1,\,3 & 4 \\ 4& 1,\,1,\,4 & 1,\,1,\,4 & 6 \end{array}$$ The only possible values for $\lfloor x\rfloor+\lfloor y\rfloor+\lfloor z\rfloor$ are $4$, $5$ and $6$. If I read the question correctly, it asks for the sum of those values, which is $15.$[/sp]

Edit. I like Serena beat me by just seconds!

 

[I like Serena]

Re: Evaluate ⌊x⌋+⌊y⌋+⌊z⌋

Edit. I like Serena beat me by just seconds!

We can only see that we posted in the same minute.

Let $x$ be the time I like Serena posted in minutes, and let $y$ be the time Opalg posted.
Then we know that $⌊x⌋=⌊y⌋$ and also that $x<y$.
Therefore $0 < y-x < 60 \text{ s}$.
Note that a smaller amount is more likely, since with higher amounts the probability increases that we'd have posted in different minutes.
The leaves the question what the expected time difference is. ;)

 

[anemone]

Re: Evaluate ⌊x⌋+⌊y⌋+⌊z⌋

Hey I like Serena and Opalg,

Thank you so so much for participating! At first I thought that folks are jaded with me already... getting bored because I posted almost a challenge a day here without fail. To be completely candid, sometimes, I even ask Mark if it's appropriate for me to keep posting!

Solution which I found along with the problem:

Spoiler

$6=x+y+z$

$3=(x-1)+(y-1)+(z-1)<\lfloor x \rfloor+\lfloor y \rfloor+\lfloor z \rfloor \le \lfloor x+y+z \rfloor=6$

$\therefore \lfloor x \rfloor+\lfloor y \rfloor+\lfloor z \rfloor=4, 5, 6$

and hence $\lfloor x \rfloor+\lfloor y \rfloor+\lfloor z \rfloor=4+5+6=15$.

We can only see that we posted in the same minute.

Let $x$ be the time I like Serena posted in minutes, and let $y$ be the time Opalg posted.
Then we know that $⌊x⌋=⌊y⌋$ and also that $x<y$.
Therefore $0 < y-x < 60 \text{ s}$.
Note that a smaller amount is more likely, since with higher amount the probability increases that we'd have posted in different minutes.
The leaves the question what the expected time difference is. ;)

I laughed out loud (more than once) when I read this, I like Serena, you have a wonderful personality and a sense of humor!