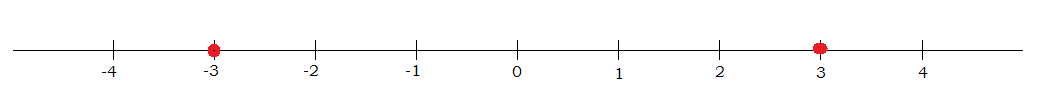What is the Factorization and Inequality of a Lagoon's Depth Function?

[noahpww]

Hello Everybody ,

First of all, I would like to apologize that this problem contains 3 parts to it (3 questions) but they all relate to each other. You must complete one part to move on to the next part. With that being said, I have 3-part problem that I could use some assistance with.

1a. Suppose a sonar device is set-up in the middle of a lagoon. The device found the depth of the lagoon in feet, as a function of the horizontal distance, in yards, from the device is given by D(x) = (x² − 4)³ − 5(x² − 4)² + (x² − 4) − 5. Factor the formula for D completely. Do not solve for anything.

I tried factoring this and got D(x) = (x + 3)(x - 3)(x^4 − 8^2 + 17) Is this correct?

1b. Draw and complete a number line for the inequality D(x) > 0.

How would I got about creating a number line for this?

1c. Assuming the lagoon is circular, using the information from your number line in part (b), what is the diameter of the pond?

(A side not for this entire 3-part problem, D(x)=0 is at the surface of the lagoon. Assume the positive direction to be "upwards.")

 

[MarkFL]

Okay, we are given:

$$D(x)=(x^2-4)^3-5(x^2-4)^2+(x^2-4)-5=(x^2-4)^2(x^2-9)+(x^2-9)=(x^2-9)((x^2-4)^2+1)=(x+3)(x-3)(x^4-8x^2+17)\quad\checkmark$$

We see that the factor that's a quadratic in $x^2$ has a negative discriminant, so the only real roots are:

$$x=\pm3$$

So, what you want to do is draw a number line and plot those two real roots on the line, and then pick a test value from one of the resulting intervals to determine the sign of $D$ in that interval. Since both of these roots are of multiplicity 1 (an odd multiplicity) we know the sign of $D$ will alternate across the 3 intervals. I would choose the middle interval, which is $(-3,3)$ and use zero as the test point.

What is the sign of $D(0)$?

 

[noahpww]

Mark,

I'm sorry but I'm confused by this question.

 

[MarkFL]

We found that the only real roots of $D$ are at $x=\pm3$, or:

$$D(-3)=D(3)=0$$

This means that as $x$ moves across those two roots, the function $D$ changes sign. So, what I would do is draw a real number line and plot those two roots:

View attachment 6229

Okay, now we can pick a test value from any 1 of the resulting three intervals:

$$(-\infty,-3),\,(-3,3),\,(3,\infty)$$

For simplicity, I would choose the middle interval and let the test point be $x=0$. Now, we see that if $x=0$, then our factored form of $D$ will have 2 positive factors and a negative factor, which means:

$$D(0)<0$$

Thus, because the sign of $D$ will alternate across the 3 intervals, we know we must have:

View attachment 6230

The diameter of the lagoon will be the distance between the roots...which is?

 

[noahpww]

Would it be 5 feet since there are 5 intervals between -3 & 3 (-2,-1,0,1,2)?

 

[MarkFL]

No it would be the distance from -3 to 3, which is 6 yards. Recall the horizontal distances are in yards, while vertical distances are in feet. :D

 

[zzephod]

1a. Suppose a sonar device is set-up in the middle of a lagoon. The device found the depth of the lagoon in feet, as a function of the horizontal distance, in yards, from the device is given by D(x) = (x² − 4)³ − 5(x² − 4)² + (x² − 4) − 5. Factor the formula for D completely. Do not solve for anything.

We want to factor $$(x² − 4)³ − 5(x² − 4)² + (x² − 4) − 5$$
First put $y=x^2-4$, then we are looking to factor $y^3-5y^2+y-5$, which is obviously zero when $y=5$, so $(y-5)$ is a factor of this. Taking this factor out gives us $$(y-5)(y^2+1)$$

The second bracketed term obviously has no real roots, so when we back substitute $(x^2-4)$ for $y$ in this term, what we have still has no real roots, and so no real factors. Doing the back substitution on the whole thing gives:
$$(x^2-9)[ (x^2-4)^2+1 ]=(x-3)(x+3)[x^4-8x^2+17]$$
Which is a complete factorization as we know the term in the square bracket has no real factors.

 

[noahpww]

Mark,

Oh okay this makes sense. Thank you so much for your help. I really appreciate it!