Discussion Overview
The discussion revolves around the impact of discontinuous potentials on quantum harmonic oscillators, exploring the relationship between quantum mechanics and nuclear physics. Participants examine various potential energy functions, the applicability of harmonic oscillator models to different particles, and the implications of using approximations like square wells in quantum systems.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
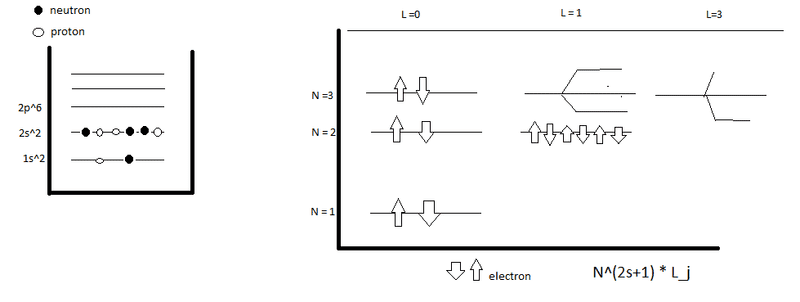
- Some participants question whether neutrons or electrons are the oscillating particles in the context of harmonic oscillators.
- There is confusion about the separation of nuclear physics from quantum physics, particularly in relation to the strong force.
- Participants discuss the determination of polynomials related to quantum numbers and their connection to electronic configurations versus the shell model.
- One participant clarifies that the harmonic oscillator applies to the eigenvalues and eigenstates of a potential, not directly to particles, and can be applied to both neutrons and electrons depending on the chosen potential.
- There is a discussion about the potential energy functions for different systems, including the harmonic oscillator and the hydrogen atom, with a request for clarification on the potential energy function for square wells related to nuclear forces.
- Some participants argue that square wells are approximations that do not accurately reflect reality due to discontinuities, and discuss the implications of a step potential and its associated forces.
- One participant notes that while the step potential is a useful toy model, it is unphysical and lacks considerations for other forces like Coulomb and centrifugal potentials.
Areas of Agreement / Disagreement
Participants express multiple competing views regarding the applicability of harmonic oscillators to different particles and the nature of potential energy functions. The discussion remains unresolved with no consensus on the best approach or model.
Contextual Notes
Limitations include the dependence on specific definitions of potentials, the approximation nature of square wells, and the unresolved mathematical implications of discontinuous potentials.