Quantum Harmonic Oscillator (QHO)

[Abdul Quader]

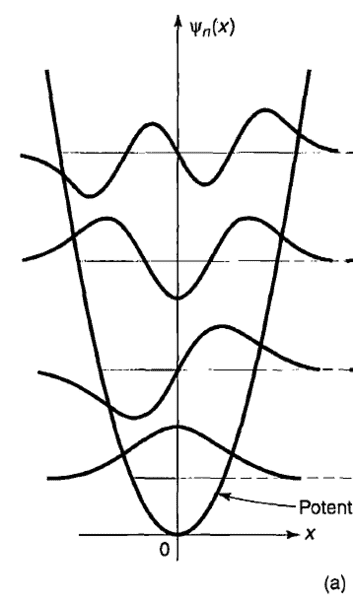
1. I have been trying to plot wavefunctions of QHO for different states with potential energy function using excel. I followed Griffith's Quantum Mechanics, 2nd edition. I got the nature but they have same reference level. Basically I tried to draw fig2.7a (the first one) and got like the second picture.

2. Why does quantum harmonic oscillator need to be solved around singular points for which frobenius technique is used?

3. What is reason behind the fact that the coefficient of highest power should be equal to 2^n to be a hermite polynomial? (Ajay Ghatak, Fundamental Theories of Physics, page 166, article 7.3)

4. Why is one of the even and odd series forced to rather not making mathematically zero in case of getting hermite polynomial? (Ajay Ghatak, Fundamental Theories of Physics, page 166, article 7.3)

 

[vanhees71]

Ad 1) You just have to shift each wave function up by a certain amount to get the figure as in the textbook (which I always found a very misleading way to plot, but that may be personal).

Ad 2) The Frobenius method is quite cumbersome for the harmonic oscillator. The point is that you have to find the square-integrable solutions of the energy-eigenvalue equation (aka time-independent Schrödinger equation). The singular points are at infinity, and you usually start with the asymptotic behavior of the equation leading to the ansatz $\psi(x)=\chi(x) \exp(-a x^2)$ (with $a$ the appropriate constant you get from the differential equation). Then you use the power-series ansatz to solve the differential equation for $\chi$. As it turns out, these series must be finite, i.e., a polynom to get square-integrable solutions only, and the demand that the series ends at a given power leads to the discrete energy-eigenvalues of the harmonic oscillator Hamiltonian, $E_{n}=(2n+1) \hbar \omega/2$, $n \in\{0,1,2,\ldots \}$.

Ad 3) The normalization is arbitrary and usually chosen by convenience or just by tradition. For the Hermite polynomials it's just convenient, because then you can define them as (physicists' convention)
$$\mathrm{H}_n(x)=(-1)^n \exp x^2 \mathrm{d}_x^n \exp(-x^2).$$

Ad 4) You just want to find all eigenvalues and the corresponding eigenfunctions of the Hamiltonian. Since the Hamiltonian is invariant under space reflections, the eigenfunctions can be chosen to be even or odd (i.e., you can define a set of common eigenfunctions of energy and parity). To know this beforehand, facilitates the finding of the eigenvalues with the Frobenius method considerable. Since for the simple harmonic oscillator the energy eigenvalues are non-degenerate the eigenfunctions are unique for each eigenvalue, and thus by themselves necessarily a parity eigenstate. They are alternately even and odd under parity, with $\psi_n(-x)=(-1)^n \psi(x)$.

A much more convenient method to solve for the harmonic oscillator is to first solve it in a completely algebraic approach, introducing ladder operators. This also immediately leads to the above given formula for the Hermite polynomials by iteration.

 

[Abdul Quader]

Thanks for the reply. Some of I understand and some of I don't. Can you suggest some text to study Hermite polynomial leading to the answers?

 

[vanhees71]

The treatment I have in mind can be found in the textbook by Sakurai:

J. J. Sakurai, S. F. Tuan, Modern Quantum Mechanics, Revised Edition, Addison-Wesley (1993)

I guess that you also find it in the later edition with Napolitano as co-author, but I cannot check this right now.

 

[Abdul Quader]

Thanks. i didn't check this text although I have this. Since I was going through Griffith's rigorously and tried to stick to it. I will check it now.

 

[vanhees71]

Well, I've the impression that Griffiths's book on QM is not the best to study from.