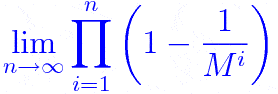SUMMARY
The discussion centers on determining the lower and upper bounds for the infinite product term \(\prod_{i=1}^{\infty}\left(1-\frac{1}{M^{i}}\right)\) where \(M \geq 2\). Participants confirm that the product converges strictly above zero and provide methods for establishing upper bounds using logarithmic transformations and series expansions. Specifically, they derive that \(\prod_{n=1}^{\infty} (1-m^{-n}) < e^{-m/(m-1)^2}\) for \(M > 1\), ensuring that the product does not converge to zero.
PREREQUISITES
- Understanding of infinite products and convergence criteria
- Familiarity with logarithmic functions and series expansions
- Knowledge of the Q-Pochhammer symbol and its applications
- Basic principles of probability, particularly Bernoulli trials
NEXT STEPS
- Explore the properties of the Q-Pochhammer symbol in combinatorial contexts
- Study the convergence of infinite products in mathematical analysis
- Learn about Euler's function and its significance in number theory
- Investigate advanced techniques for bounding series and products
USEFUL FOR
Mathematicians, statisticians, and researchers in combinatorial analysis or number theory who are interested in infinite products and their convergence properties.