Shah 72
MHB
- 274
- 0
A particle moves on a straight line. It starts at a point O on the line and returns to O 100 s later. The velocity of P is v m/s at time t s after leaving O where v= 0.000t^3- 0.015t^2 +0.5t.
1) Find the values of v at the times for which the acceleration of P is zero
I got when t= 21.1s, V= 4.81m/s and when t= 78.9s v= -4.81m/s
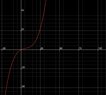
2) sketch the velocity time graph for Ps motion for 0<t<100
So I plotted for t=0 v=0, t= 21.1 v=4.81, t= 78.9, v= -4.81 and t=100, v=0. So it will be two curves with the curve going up between 0 and 50 and curve going down between 50 and 100.
Is this right??
3) Find the greatest distance of P from 0 for 0<t<100
I don't understand this part.
1) Find the values of v at the times for which the acceleration of P is zero
I got when t= 21.1s, V= 4.81m/s and when t= 78.9s v= -4.81m/s
2) sketch the velocity time graph for Ps motion for 0<t<100
So I plotted for t=0 v=0, t= 21.1 v=4.81, t= 78.9, v= -4.81 and t=100, v=0. So it will be two curves with the curve going up between 0 and 50 and curve going down between 50 and 100.
Is this right??
3) Find the greatest distance of P from 0 for 0<t<100
I don't understand this part.