anemone
Gold Member
MHB
POTW Director
- 3,851
- 115
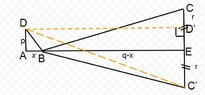
For positive real numbers $p,\,q,\,r$, determine the minimum of the function $f(x)=\sqrt{p^2+x^2}+\sqrt{(q-x)^2+r^2}$.